Quantized Wasserstein Procrustes Alignment of Word Embedding Spaces

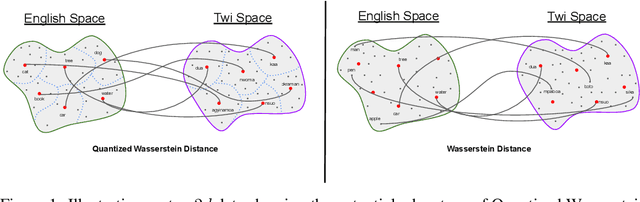
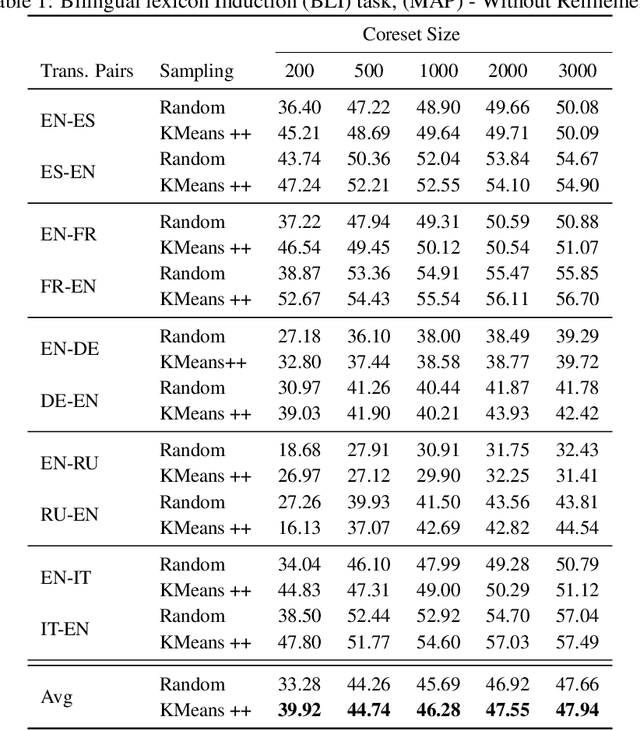
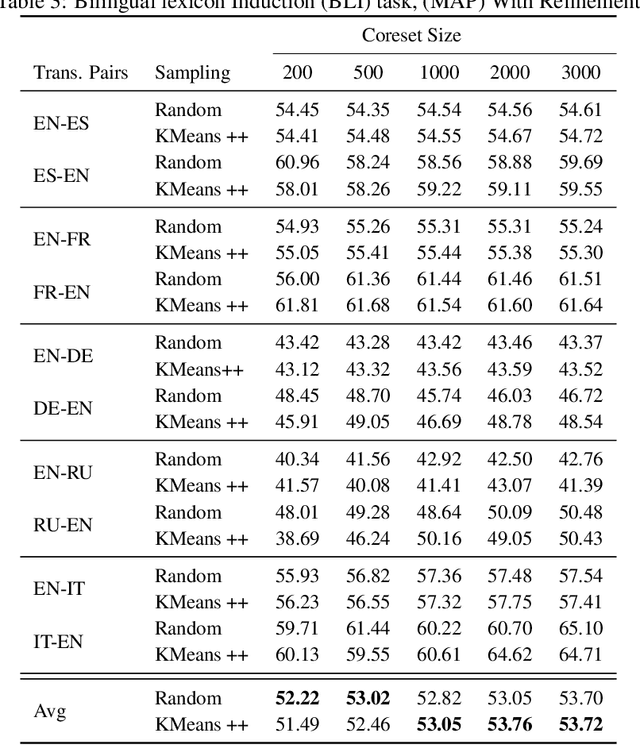
Optimal Transport (OT) provides a useful geometric framework to estimate the permutation matrix under unsupervised cross-lingual word embedding (CLWE) models that pose the alignment task as a Wasserstein-Procrustes problem. However, linear programming algorithms and approximate OT solvers via Sinkhorn for computing the permutation matrix come with a significant computational burden since they scale cubically and quadratically, respectively, in the input size. This makes it slow and infeasible to compute OT distances exactly for a larger input size, resulting in a poor approximation quality of the permutation matrix and subsequently a less robust learned transfer function or mapper. This paper proposes an unsupervised projection-based CLWE model called quantized Wasserstein Procrustes (qWP). qWP relies on a quantization step of both the source and target monolingual embedding space to estimate the permutation matrix given a cheap sampling procedure. This approach substantially improves the approximation quality of empirical OT solvers given fixed computational cost. We demonstrate that qWP achieves state-of-the-art results on the Bilingual lexicon Induction (BLI) task.

On Measuring and Mitigating Biased Inferences of Word Embeddings

Word embeddings carry stereotypical connotations from the text they are trained on, which can lead to invalid inferences. We use this observation to design a mechanism for measuring stereotypes using the task of natural language inference. We demonstrate a reduction in invalid inferences via bias mitigation strategies on static word embeddings (GloVe), and explore adapting them to contextual embeddings (ELMo).

Learning In Practice: Reasoning About Quantization

There is a mismatch between the standard theoretical analyses of statistical machine learning and how learning is used in practice. The foundational assumption supporting the theory is that we can represent features and models using real-valued parameters. In practice, however, we do not use real numbers at any point during training or deployment. Instead, we rely on discrete and finite quantizations of the reals, typically floating points. In this paper, we propose a framework for reasoning about learning under arbitrary quantizations. Using this formalization, we prove the convergence of quantization-aware versions of the Perceptron and Frank-Wolfe algorithms. Finally, we report the results of an extensive empirical study of the impact of quantization using a broad spectrum of datasets.

Attenuating Bias in Word Vectors

Word vector representations are well developed tools for various NLP and Machine Learning tasks and are known to retain significant semantic and syntactic structure of languages. But they are prone to carrying and amplifying bias which can perpetrate discrimination in various applications. In this work, we explore new simple ways to detect the most stereotypically gendered words in an embedding and remove the bias from them. We verify how names are masked carriers of gender bias and then use that as a tool to attenuate bias in embeddings. Further, we extend this property of names to show how names can be used to detect other types of bias in the embeddings such as bias based on race, ethnicity, and age.