Quantized Wasserstein Procrustes Alignment of Word Embedding Spaces
Paper and Code
Dec 05, 2022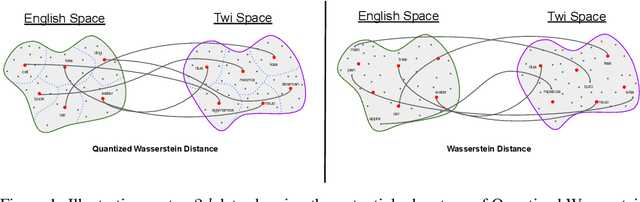
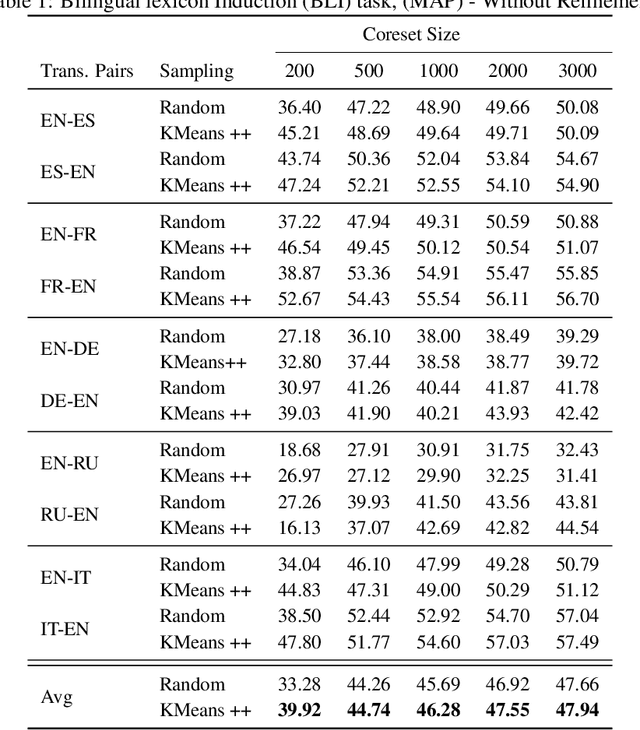

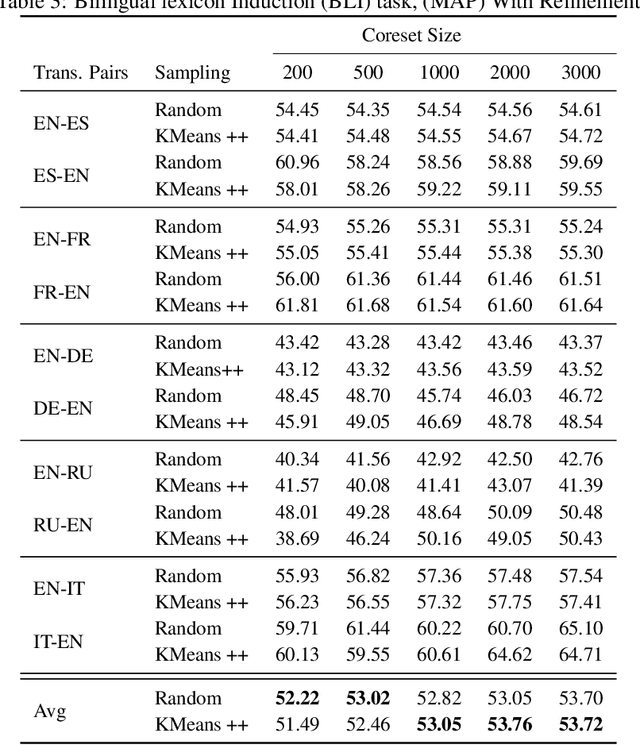
Optimal Transport (OT) provides a useful geometric framework to estimate the permutation matrix under unsupervised cross-lingual word embedding (CLWE) models that pose the alignment task as a Wasserstein-Procrustes problem. However, linear programming algorithms and approximate OT solvers via Sinkhorn for computing the permutation matrix come with a significant computational burden since they scale cubically and quadratically, respectively, in the input size. This makes it slow and infeasible to compute OT distances exactly for a larger input size, resulting in a poor approximation quality of the permutation matrix and subsequently a less robust learned transfer function or mapper. This paper proposes an unsupervised projection-based CLWE model called quantized Wasserstein Procrustes (qWP). qWP relies on a quantization step of both the source and target monolingual embedding space to estimate the permutation matrix given a cheap sampling procedure. This approach substantially improves the approximation quality of empirical OT solvers given fixed computational cost. We demonstrate that qWP achieves state-of-the-art results on the Bilingual lexicon Induction (BLI) task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge