Jeff A. Bilmes
Faster graphical model identification of tandem mass spectra using peptide word lattices
Oct 29, 2014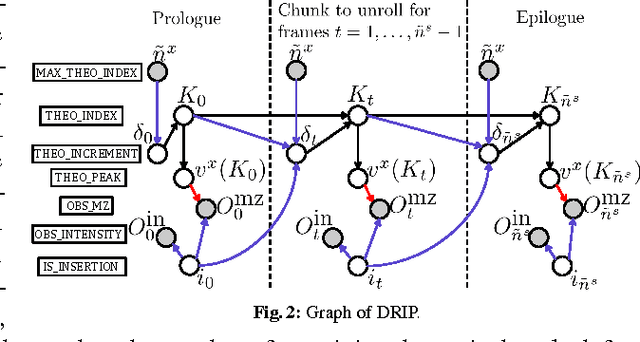

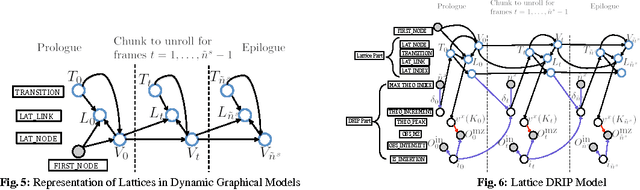
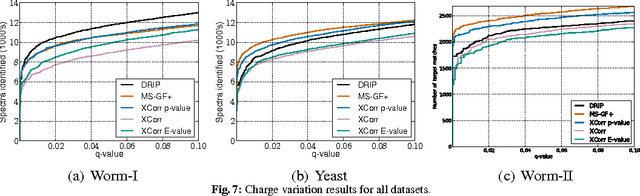
Abstract:Liquid chromatography coupled with tandem mass spectrometry, also known as shotgun proteomics, is a widely-used high-throughput technology for identifying proteins in complex biological samples. Analysis of the tens of thousands of fragmentation spectra produced by a typical shotgun proteomics experiment begins by assigning to each observed spectrum the peptide hypothesized to be responsible for generating the spectrum, typically done by searching each spectrum against a database of peptides. We have recently described a machine learning method---Dynamic Bayesian Network for Rapid Identification of Peptides (DRIP)---that not only achieves state-of-the-art spectrum identification performance on a variety of datasets but also provides a trainable model capable of returning valuable auxiliary information regarding specific peptide-spectrum matches. In this work, we present two significant improvements to DRIP. First, we describe how to use word lattices, which are widely used in natural language processing, to significantly speed up DRIP's computations. To our knowledge, all existing shotgun proteomics search engines compute independent scores between a given observed spectrum and each possible candidate peptide from the database. The key idea of the word lattice is to represent the set of candidate peptides in a single data structure, thereby allowing sharing of redundant computations among the different candidates. We demonstrate that using lattices in conjunction with DRIP leads to speedups on the order of tens across yeast and worm data sets. Second, we introduce a variant of DRIP that uses a discriminative training framework, performing maximum mutual entropy estimation rather than maximum likelihood estimation. This modification improves DRIP's statistical power, enabling us to increase the number of identified spectrum at a 1% false discovery rate on yeast and worm data sets.
The Lovasz-Bregman Divergence and connections to rank aggregation, clustering, and web ranking
Aug 09, 2014

Abstract:We extend the recently introduced theory of Lovasz-Bregman (LB) divergences (Iyer & Bilmes 2012) in several ways. We show that they represent a distortion between a "score" and an "ordering", thus providing a new view of rank aggregation and order based clustering with interesting connections to web ranking. We show how the LB divergences have a number of properties akin to many permutation based metrics, and in fact have as special cases forms very similar to the Kendall-tau metric. We also show how the LB divergences subsume a number of commonly used ranking measures in information retrieval, like NDCG and AUC. Unlike the traditional permutation based metrics, however, the LB divergence naturally captures a notion of "confidence" in the orderings, thus providing a new representation to applications involving aggregating scores as opposed to just orderings. We show how a number of recently used web ranking models are forms of Lovasz-Bregman rank aggregation and also observe that a natural form of Mallow's model using the LB divergence has been used as conditional ranking models for the "Learning to Rank" problem.
Algorithms for Approximate Minimization of the Difference Between Submodular Functions, with Applications
Aug 09, 2014



Abstract:We extend the work of Narasimhan and Bilmes [30] for minimizing set functions representable as a dierence between submodular functions. Similar to [30], our new algorithms are guaranteed to monotonically reduce the objective function at every step. We empirically and theoretically show that the per-iteration cost of our algorithms is much less than [30], and our algorithms can be used to efficiently minimize a dierence between submodular functions under various combinatorial constraints, a problem not previously addressed. We provide computational bounds and a hardness result on the multiplicative inapproximability of minimizing the dierence between submodular functions. We show, however, that it is possible to give worst-case additive bounds by providing a polynomial time computable lower-bound on the minima. Finally we show how a number of machine learning problems can be modeled as minimizing the dierence between submodular functions. We experimentally show the validity of our algorithms by testing them on the problem of feature selection with submodular cost features.
Dynamic Bayesian Multinets
Jan 16, 2013



Abstract:In this work, dynamic Bayesian multinets are introduced where a Markov chain state at time t determines conditional independence patterns between random variables lying within a local time window surrounding t. It is shown how information-theoretic criterion functions can be used to induce sparse, discriminative, and class-conditional network structures that yield an optimal approximation to the class posterior probability, and therefore are useful for the classification task. Using a new structure learning heuristic, the resulting models are tested on a medium-vocabulary isolated-word speech recognition task. It is demonstrated that these discriminatively structured dynamic Bayesian multinets, when trained in a maximum likelihood setting using EM, can outperform both HMMs and other dynamic Bayesian networks with a similar number of parameters.
On Triangulating Dynamic Graphical Models
Oct 19, 2012



Abstract:This paper introduces new methodology to triangulate dynamic Bayesian networks (DBNs) and dynamic graphical models (DGMs). While most methods to triangulate such networks use some form of constrained elimination scheme based on properties of the underlying directed graph, we find it useful to view triangulation and elimination using properties only of the resulting undirected graph, obtained after the moralization step. We first briefly introduce the Graphical model toolkit (GMTK) and its notion of dynamic graphical models, one that slightly extends the standard notion of a DBN. We next introduce the 'boundary algorithm', a method to find the best boundary between partitions in a dynamic model. We find that using this algorithm, the notions of forward- and backward-interface become moot - namely, the size and fill-in of the best forward- and backward- interface are identical. Moreover, we observe that finding a good partition boundary allows for constrained elimination orders (and therefore graph triangulations) that are not possible using standard slice-by-slice constrained eliminations. More interestingly, with certain boundaries it is possible to obtain constrained elimination schemes that lie outside the space of possible triangulations using only unconstrained elimination. Lastly, we report triangulation results on invented graphs, standard DBNs from the literature, novel DBNs used in speech recognition research systems, and also random graphs. Using a number of different triangulation quality measures (max clique size, state-space, etc.), we find that with our boundary algorithm the triangulation quality can dramatically improve.
Learning Mixtures of Submodular Shells with Application to Document Summarization
Oct 16, 2012



Abstract:We introduce a method to learn a mixture of submodular "shells" in a large-margin setting. A submodular shell is an abstract submodular function that can be instantiated with a ground set and a set of parameters to produce a submodular function. A mixture of such shells can then also be so instantiated to produce a more complex submodular function. What our algorithm learns are the mixture weights over such shells. We provide a risk bound guarantee when learning in a large-margin structured-prediction setting using a projected subgradient method when only approximate submodular optimization is possible (such as with submodular function maximization). We apply this method to the problem of multi-document summarization and produce the best results reported so far on the widely used NIST DUC-05 through DUC-07 document summarization corpora.
PAC-learning bounded tree-width Graphical Models
Jul 11, 2012
Abstract:We show that the class of strongly connected graphical models with treewidth at most k can be properly efficiently PAC-learnt with respect to the Kullback-Leibler Divergence. Previous approaches to this problem, such as those of Chow ([1]), and Ho gen ([7]) have shown that this class is PAC-learnable by reducing it to a combinatorial optimization problem. However, for k > 1, this problem is NP-complete ([15]), and so unless P=NP, these approaches will take exponential amounts of time. Our approach differs significantly from these, in that it first attempts to find approximate conditional independencies by solving (polynomially many) submodular optimization problems, and then using a dynamic programming formulation to combine the approximate conditional independence information to derive a graphical model with underlying graph of the tree-width specified. This gives us an efficient (polynomial time in the number of random variables) PAC-learning algorithm which requires only polynomial number of samples of the true distribution, and only polynomial running time.
A submodular-supermodular procedure with applications to discriminative structure learning
Jul 04, 2012



Abstract:In this paper, we present an algorithm for minimizing the difference between two submodular functions using a variational framework which is based on (an extension of) the concave-convex procedure [17]. Because several commonly used metrics in machine learning, like mutual information and conditional mutual information, are submodular, the problem of minimizing the difference of two submodular problems arises naturally in many machine learning applications. Two such applications are learning discriminatively structured graphical models and feature selection under computational complexity constraints. A commonly used metric for measuring discriminative capacity is the EAR measure which is the difference between two conditional mutual information terms. Feature selection taking complexity considerations into account also fall into this framework because both the information that a set of features provide and the cost of computing and using the features can be modeled as submodular functions. This problem is NP-hard, and we give a polynomial time heuristic for it. We also present results on synthetic data to show that classifiers based on discriminative graphical models using this algorithm can significantly outperform classifiers based on generative graphical models.
Recognizing Activities and Spatial Context Using Wearable Sensors
Jun 27, 2012

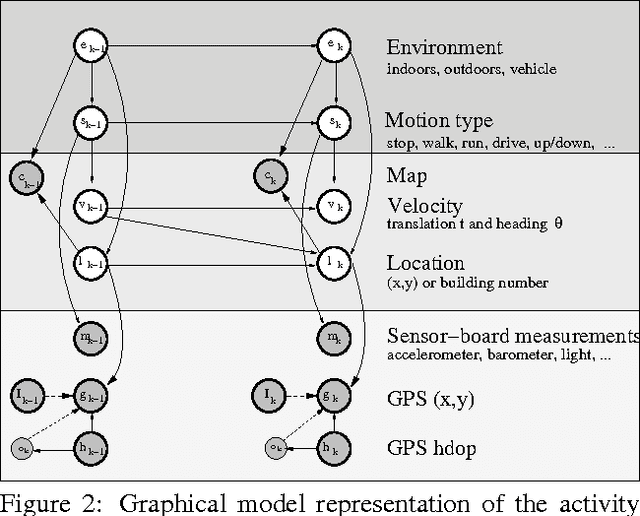

Abstract:We introduce a new dynamic model with the capability of recognizing both activities that an individual is performing as well as where that ndividual is located. Our model is novel in that it utilizes a dynamic graphical model to jointly estimate both activity and spatial context over time based on the simultaneous use of asynchronous observations consisting of GPS measurements, and measurements from a small mountable sensor board. Joint inference is quite desirable as it has the ability to improve accuracy of the model. A key goal, however, in designing our overall system is to be able to perform accurate inference decisions while minimizing the amount of hardware an individual must wear. This minimization leads to greater comfort and flexibility, decreased power requirements and therefore increased battery life, and reduced cost. We show results indicating that our joint measurement model outperforms measurements from either the sensor board or GPS alone, using two types of probabilistic inference procedures, namely particle filtering and pruned exact inference.
Non-Minimal Triangulations for Mixed Stochastic/Deterministic Graphical Models
Jun 27, 2012



Abstract:We observe that certain large-clique graph triangulations can be useful to reduce both computational and space requirements when making queries on mixed stochastic/deterministic graphical models. We demonstrate that many of these large-clique triangulations are non-minimal and are thus unattainable via the variable elimination algorithm. We introduce ancestral pairs as the basis for novel triangulation heuristics and prove that no more than the addition of edges between ancestral pairs need be considered when searching for state space optimal triangulations in such graphs. Empirical results on random and real world graphs show that the resulting triangulations that yield significant speedups are almost always non-minimal. We also give an algorithm and correctness proof for determining if a triangulation can be obtained via elimination, and we show that the decision problem associated with finding optimal state space triangulations in this mixed stochastic/deterministic setting is NP-complete.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge