Lazy Incremental Search for Efficient Replanning with Bounded Suboptimality Guarantees

We present a lazy incremental search algorithm, Lifelong-GLS (L-GLS), along with its bounded suboptimal version, Bounded L-GLS (B-LGLS) that combine the search efficiency of incremental search algorithms with the evaluation efficiency of lazy search algorithms for fast replanning in problem domains where edge-evaluations are more expensive than vertex-expansions. The proposed algorithms generalize Lifelong Planning A* (LPA*) and its bounded suboptimal version, Truncated LPA* (TLPA*), within the Generalized Lazy Search (GLS) framework, so as to restrict expensive edge evaluations only to the current shortest subpath when the cost-to-come inconsistencies are propagated during repair. We also present dynamic versions of the L-GLS and B-LGLS algorithms, called Generalized D* (GD*) and Bounded Generalized D* (B-GD*), respectively, for efficient replanning with non-stationary queries, designed specifically for navigation of mobile robots. We prove that the proposed algorithms are complete and correct in finding a solution that is guaranteed not to exceed the optimal solution cost by a user-chosen factor. Our numerical and experimental results support the claim that the proposed integration of the incremental and lazy search frameworks can help find solutions faster compared to the regular incremental or regular lazy search algorithms when the underlying graph representation changes often.

Information-theoretic Abstraction of Semantic Octree Models for Integrated Perception and Planning

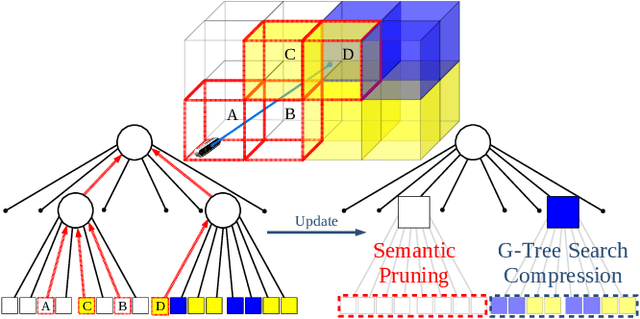
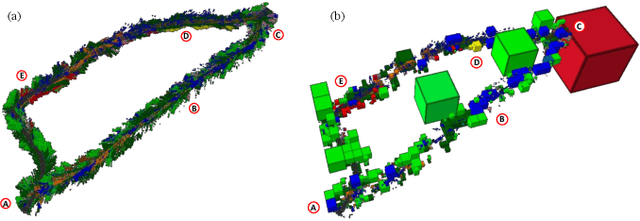
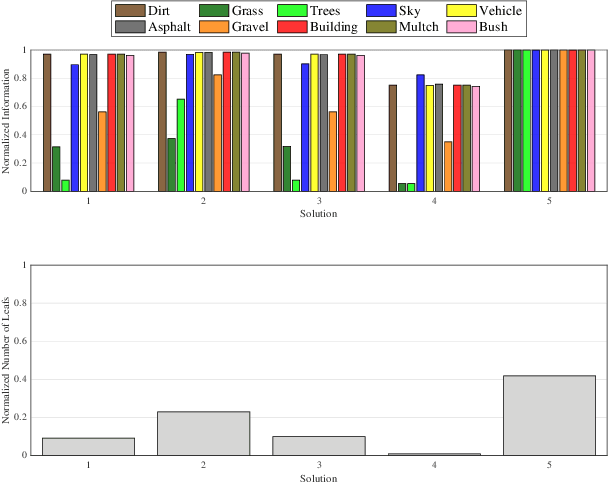
In this paper, we develop an approach that enables autonomous robots to build and compress semantic environment representations from point-cloud data. Our approach builds a three-dimensional, semantic tree representation of the environment from sensor data which is then compressed by a novel information-theoretic tree-pruning approach. The proposed approach is probabilistic and incorporates the uncertainty in semantic classification inherent in real-world environments. Moreover, our approach allows robots to prioritize individual semantic classes when generating the compressed trees, so as to design multi-resolution representations that retain the relevant semantic information while simultaneously discarding unwanted semantic categories. We demonstrate the approach by compressing semantic octree models of a large outdoor, semantically rich, real-world environment. In addition, we show how the octree abstractions can be used to create semantically-informed graphs for motion planning, and provide a comparison of our approach with uninformed graph construction methods such as Halton sequences.

CBS-Budget : A Complete and Bounded Suboptimal Search for Multi-Agent Path Finding

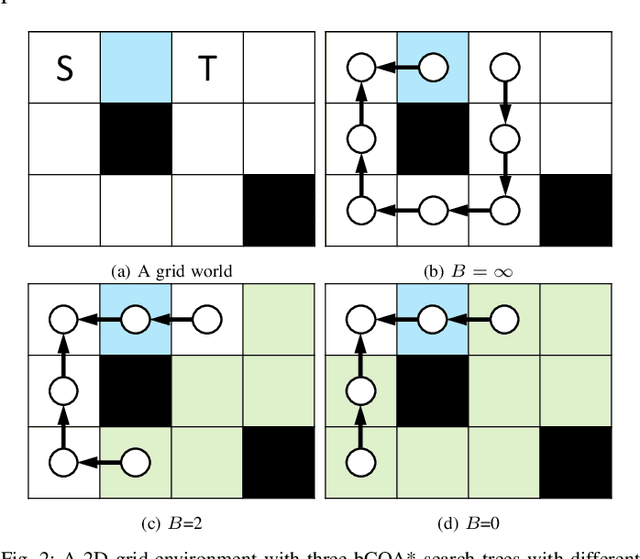
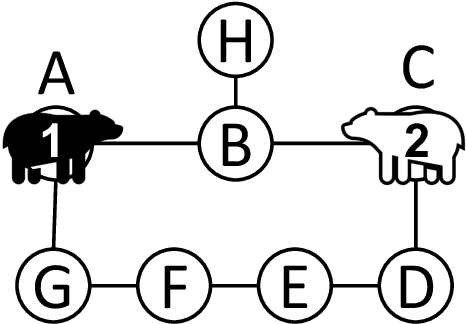
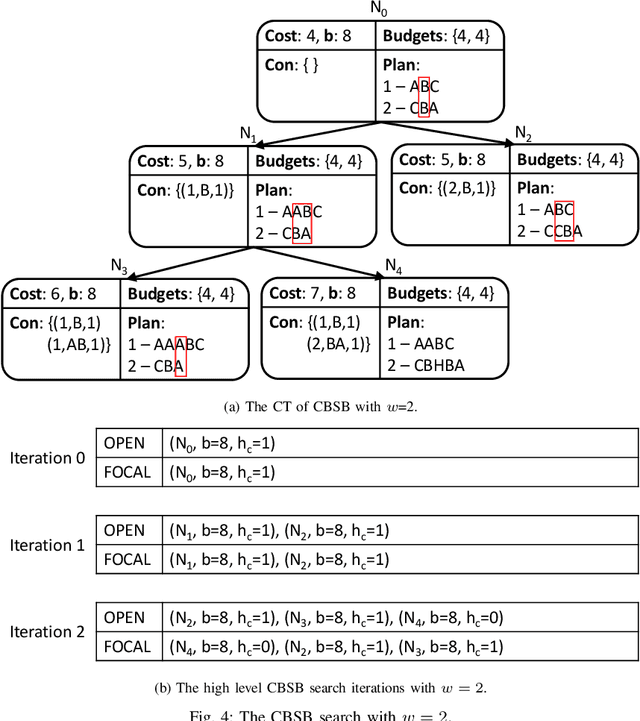
Multi-Agent Path Finding (MAPF) is the problem of finding a collection of collision-free paths for a team of multiple agents while minimizing some global cost, such as the sum of the time travelled by all agents, or the time travelled by the last agent. Conflict Based Search (CBS) is a leading complete and optimal MAPF solver which lazily explores the joint agent state space, using an admissible heuristic joint plan. Such an admissible heuristic joint plan is computed by combining individual shortest paths found without considering inter-agent conflicts, and which becomes gradually more informed as constraints are added to individual agents' path planning problems to avoid discovered conflicts. In this paper, we seek to speedup CBS by finding a more informed heuristic joint plan which is bounded from above. We first propose the budgeted Class-Ordered A* (bCOA*), a novel algorithm that finds the shortest path with minimal number of conflicts that is upper bounded in terms of length. Then, we propose a novel bounded-cost variant of CBS, called CBS-Budget (CBSB) by using a bCOA* search at the low-level search of the CBS and by using a modified focal search at the high-level search of the CBS. We prove that CBSB is complete and bounded-suboptimal. In our numerical experiments, CBSB finds a near optimal solution for hundreds of agents within a fraction of a second. CBSB shows state-of-the-art performance, comparable to Explicit Estimation CBS (EECBS), an enhanced recent version of CBS. On the other hand, CBSB is easier to implement than EECBS, since only two priority queues at the high-level search are needed as in Enhanced CBS (ECBS).

Lazy Lifelong Planning for Efficient Replanning in Graphs with Expensive Edge Evaluation

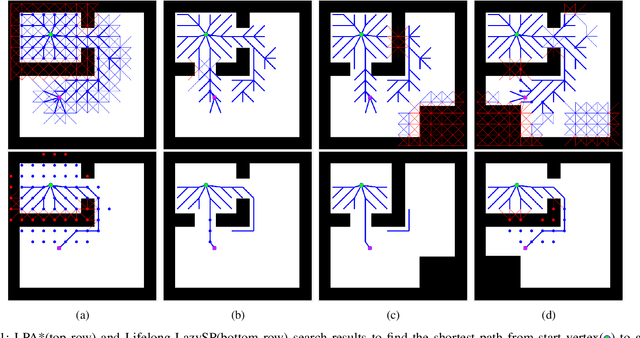
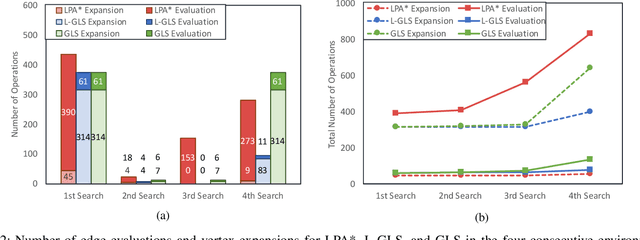
We present an incremental search algorithm, called Lifelong-GLS, which combines the vertex efficiency of Lifelong Planning A* (LPA*) and the edge efficiency of Generalized Lazy Search (GLS) for efficient replanning on dynamic graphs where edge evaluation is expensive. We use a lazily evaluated LPA* to repair the cost-to-come inconsistencies of the relevant region of the current search tree based on the previous search results, and then we restrict the expensive edge evaluations only to the current shortest subpath as in the GLS framework. The proposed algorithm is complete and correct in finding the optimal solution in the current graph, if one exists. We also show that the search returns a bounded suboptimal solution, if an inflated heuristic edge weight is used and the tree repairing propagation is truncated early for faster search. Finally, we show the efficiency of the proposed algorithm compared to the standard LPA* and the GLS algorithms over consecutive search episodes in a dynamic environment. For each search, the proposed algorithm reduces the edge evaluations by a significant amount compared to the LPA*. Both the number of vertex expansions and the number of edge evaluations are reduced substantially compared to GLS, as the proposed algorithm utilizes previous search results to facilitate the new search.

A Generalized A* Algorithm for Finding Globally Optimal Paths in Weighted Colored Graphs

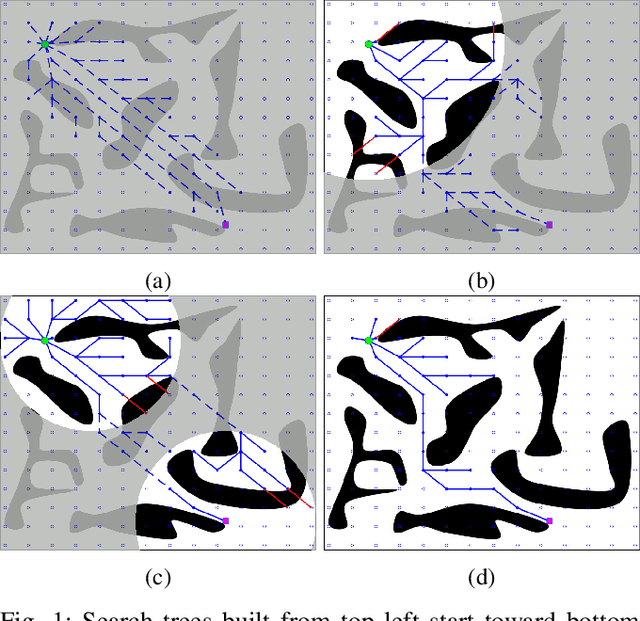
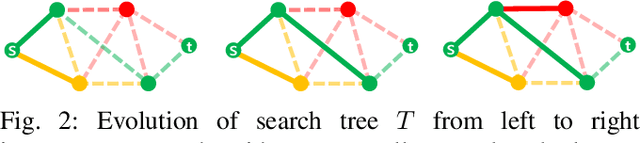
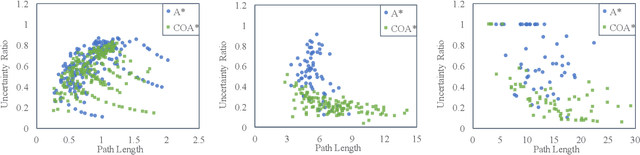
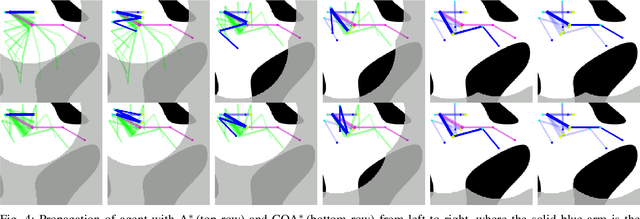
Both geometric and semantic information of the search space is imperative for a good plan. We encode those properties in a weighted colored graph (geometric information in terms of edge weight and semantic information in terms of edge and vertex color), and propose a generalized A* to find the shortest path among the set of paths with minimal inclusion of low-ranked color edges. We prove the completeness and optimality of this Class-Ordered A* (COA*) algorithm with respect to the hereto defined notion of optimality. The utility of COA* is numerically validated in a ternary graph with feasible, infeasible, and unknown vertices and edges for the cases of a 2D mobile robot, a 3D robotic arm, and a 5D robotic arm with limited sensing capabilities. We compare the results of COA* to that of the regular A* algorithm, the latter of which finds the shortest path regardless of uncertainty, and we show that the COA* dominates the A* solution in terms of finding less uncertain paths.