A Generalized A* Algorithm for Finding Globally Optimal Paths in Weighted Colored Graphs
Paper and Code
Dec 24, 2020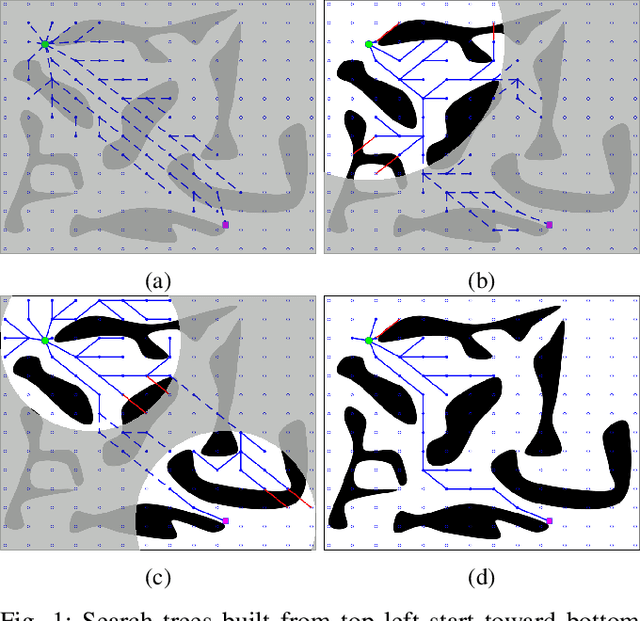
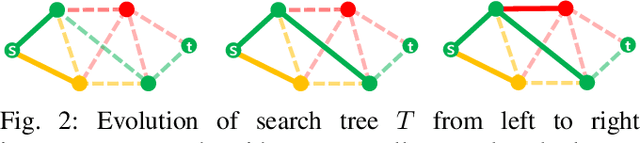
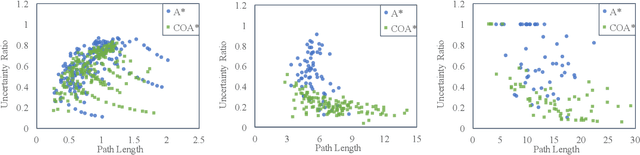
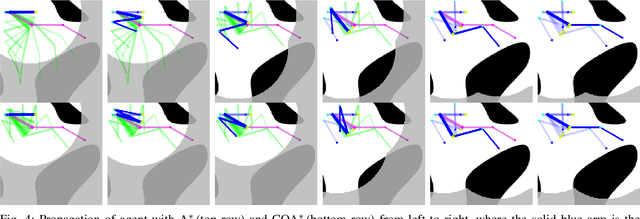
Both geometric and semantic information of the search space is imperative for a good plan. We encode those properties in a weighted colored graph (geometric information in terms of edge weight and semantic information in terms of edge and vertex color), and propose a generalized A* to find the shortest path among the set of paths with minimal inclusion of low-ranked color edges. We prove the completeness and optimality of this Class-Ordered A* (COA*) algorithm with respect to the hereto defined notion of optimality. The utility of COA* is numerically validated in a ternary graph with feasible, infeasible, and unknown vertices and edges for the cases of a 2D mobile robot, a 3D robotic arm, and a 5D robotic arm with limited sensing capabilities. We compare the results of COA* to that of the regular A* algorithm, the latter of which finds the shortest path regardless of uncertainty, and we show that the COA* dominates the A* solution in terms of finding less uncertain paths.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge