Lazy Lifelong Planning for Efficient Replanning in Graphs with Expensive Edge Evaluation
Paper and Code
May 25, 2021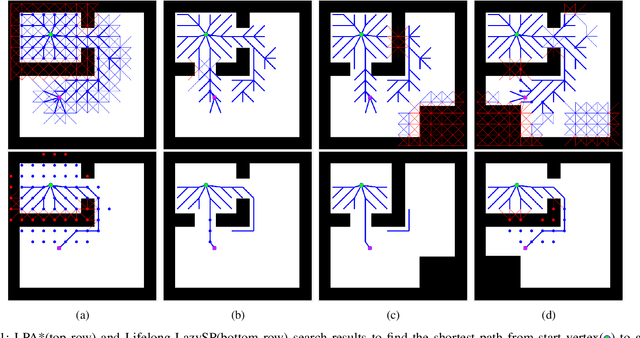
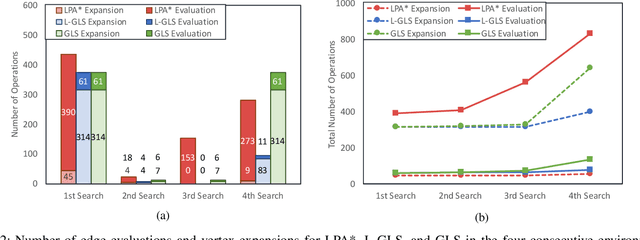

We present an incremental search algorithm, called Lifelong-GLS, which combines the vertex efficiency of Lifelong Planning A* (LPA*) and the edge efficiency of Generalized Lazy Search (GLS) for efficient replanning on dynamic graphs where edge evaluation is expensive. We use a lazily evaluated LPA* to repair the cost-to-come inconsistencies of the relevant region of the current search tree based on the previous search results, and then we restrict the expensive edge evaluations only to the current shortest subpath as in the GLS framework. The proposed algorithm is complete and correct in finding the optimal solution in the current graph, if one exists. We also show that the search returns a bounded suboptimal solution, if an inflated heuristic edge weight is used and the tree repairing propagation is truncated early for faster search. Finally, we show the efficiency of the proposed algorithm compared to the standard LPA* and the GLS algorithms over consecutive search episodes in a dynamic environment. For each search, the proposed algorithm reduces the edge evaluations by a significant amount compared to the LPA*. Both the number of vertex expansions and the number of edge evaluations are reduced substantially compared to GLS, as the proposed algorithm utilizes previous search results to facilitate the new search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge