CBS-Budget : A Complete and Bounded Suboptimal Search for Multi-Agent Path Finding

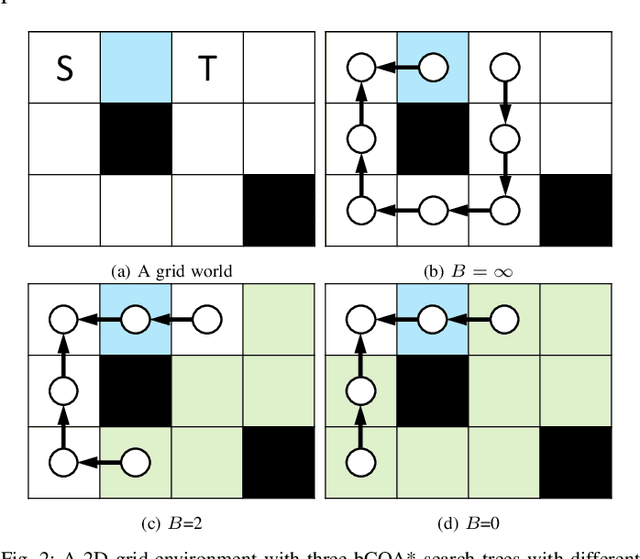
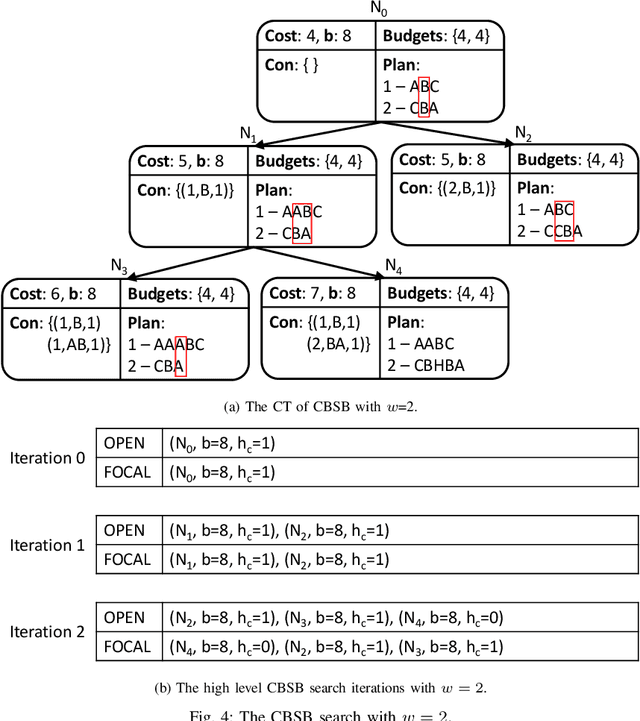
Multi-Agent Path Finding (MAPF) is the problem of finding a collection of collision-free paths for a team of multiple agents while minimizing some global cost, such as the sum of the time travelled by all agents, or the time travelled by the last agent. Conflict Based Search (CBS) is a leading complete and optimal MAPF solver which lazily explores the joint agent state space, using an admissible heuristic joint plan. Such an admissible heuristic joint plan is computed by combining individual shortest paths found without considering inter-agent conflicts, and which becomes gradually more informed as constraints are added to individual agents' path planning problems to avoid discovered conflicts. In this paper, we seek to speedup CBS by finding a more informed heuristic joint plan which is bounded from above. We first propose the budgeted Class-Ordered A* (bCOA*), a novel algorithm that finds the shortest path with minimal number of conflicts that is upper bounded in terms of length. Then, we propose a novel bounded-cost variant of CBS, called CBS-Budget (CBSB) by using a bCOA* search at the low-level search of the CBS and by using a modified focal search at the high-level search of the CBS. We prove that CBSB is complete and bounded-suboptimal. In our numerical experiments, CBSB finds a near optimal solution for hundreds of agents within a fraction of a second. CBSB shows state-of-the-art performance, comparable to Explicit Estimation CBS (EECBS), an enhanced recent version of CBS. On the other hand, CBSB is easier to implement than EECBS, since only two priority queues at the high-level search are needed as in Enhanced CBS (ECBS).