Information-theoretic Abstraction of Semantic Octree Models for Integrated Perception and Planning

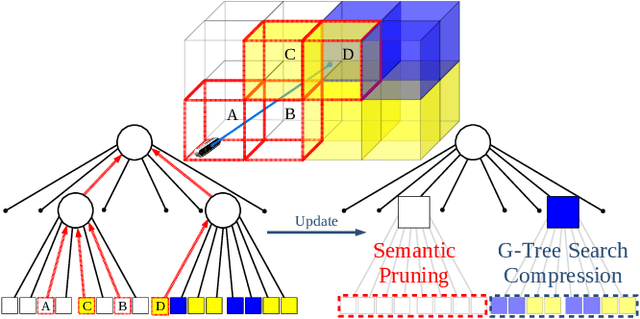
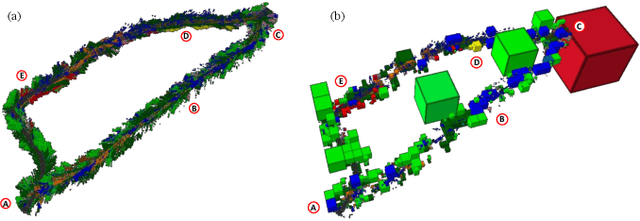
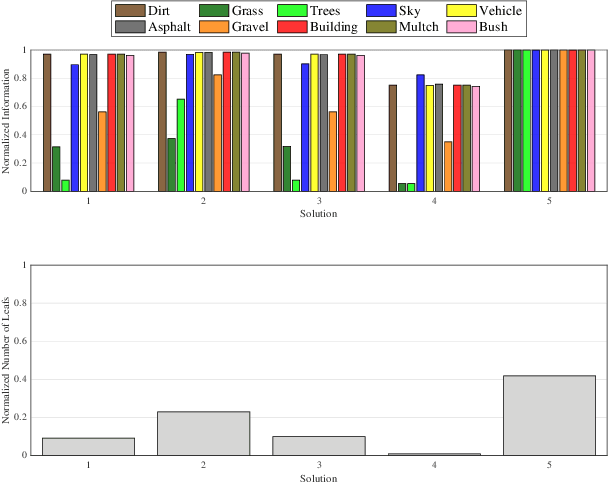
In this paper, we develop an approach that enables autonomous robots to build and compress semantic environment representations from point-cloud data. Our approach builds a three-dimensional, semantic tree representation of the environment from sensor data which is then compressed by a novel information-theoretic tree-pruning approach. The proposed approach is probabilistic and incorporates the uncertainty in semantic classification inherent in real-world environments. Moreover, our approach allows robots to prioritize individual semantic classes when generating the compressed trees, so as to design multi-resolution representations that retain the relevant semantic information while simultaneously discarding unwanted semantic categories. We demonstrate the approach by compressing semantic octree models of a large outdoor, semantically rich, real-world environment. In addition, we show how the octree abstractions can be used to create semantically-informed graphs for motion planning, and provide a comparison of our approach with uninformed graph construction methods such as Halton sequences.

A Linear Programming Approach for Resource-Aware Information-Theoretic Tree Abstractions

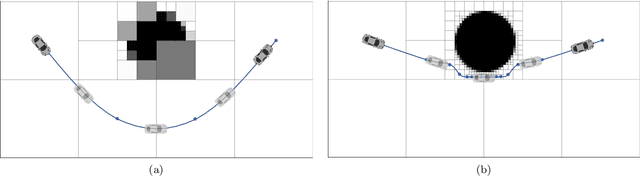
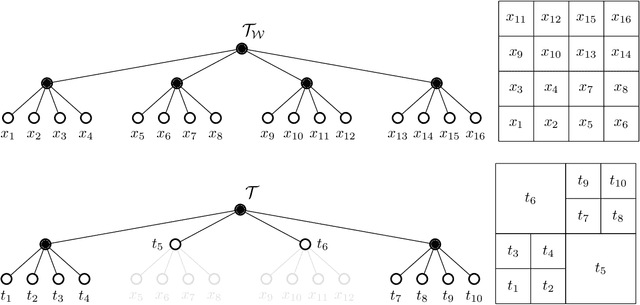
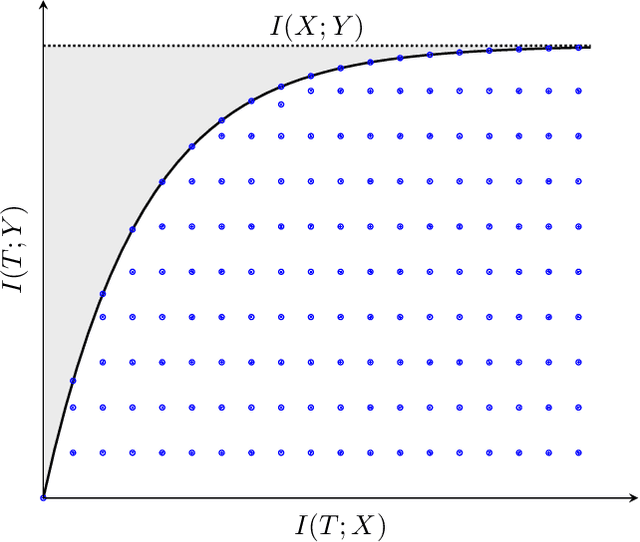
In this chapter, an integer linear programming formulation for the problem of obtaining task-relevant, multi-resolution, environment abstractions for resource-constrained autonomous agents is presented. The formulation leverages concepts from information-theoretic signal compression, specifically, the information bottleneck (IB) method, to pose an abstraction problem as an optimal encoder search over the space of multi-resolution trees. The abstractions emerge in a task-relevant manner as a function of agent information-processing constraints. We detail our formulation, and show how hierarchical tree structures, signal encoders, and information-theoretic methods for signal compression can be unified under a common theme. A discussion delineating the benefits and drawbacks of our formulation is presented, as well as a detailed explanation how our approach can be interpreted within the context of generating abstractions for resource-constrained autonomous systems. It is shown that the resulting information-theoretic abstraction problem over the space of multi-resolution trees can be formulated as a integer linear programming (ILP) problem. We demonstrate the approach on a number of examples, and provide a discussion detailing the differences of the proposed framework compared to existing methods. Lastly, we consider a linear program relaxation of the ILP problem, thereby demonstrating that multi-resolution information-theoretic tree abstractions can be obtained by solving a convex program.

Information-Theoretic Abstractions for Resource-Constrained Agents via Mixed-Integer Linear Programming

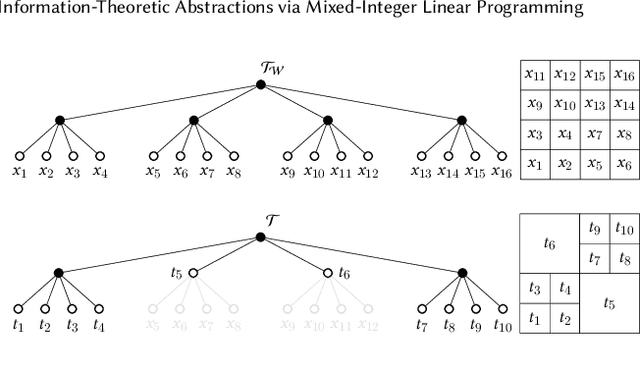
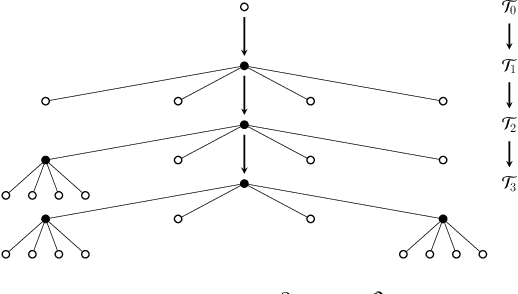
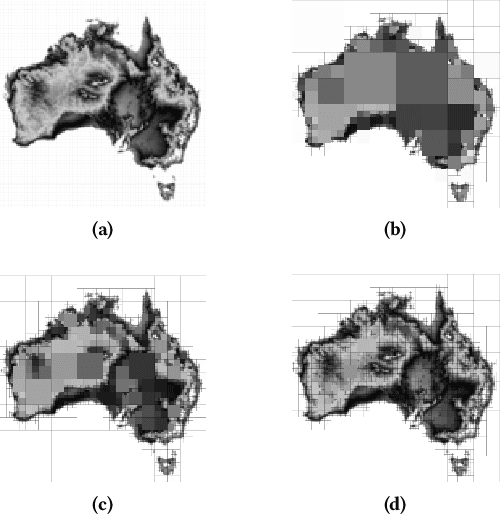
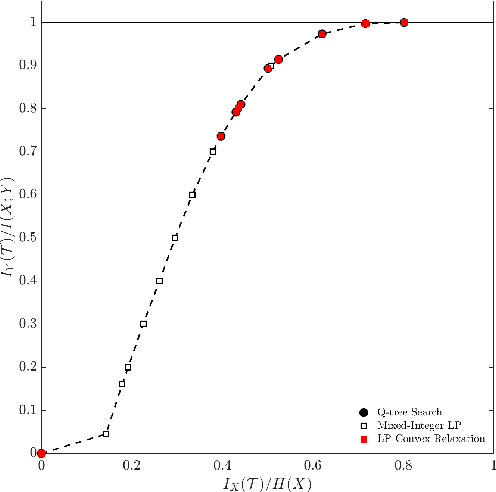
In this paper, a mixed-integer linear programming formulation for the problem of obtaining task-relevant, multi-resolution, graph abstractions for resource-constrained agents is presented. The formulation leverages concepts from information-theoretic signal compression, specifically the information bottleneck (IB) method, to pose a graph abstraction problem as an optimal encoder search over the space of multi-resolution trees. The abstractions emerge in a task-relevant manner as a function of agent information-processing constraints, and are not provided to the system a priori. We detail our formulation and show how the problem can be realized as an integer linear program. A non-trivial numerical example is presented to demonstrate the utility in employing our approach to obtain hierarchical tree abstractions for resource-limited agents.

An Information-Theoretic Approach for Path Planning in Agents with Computational Constraints

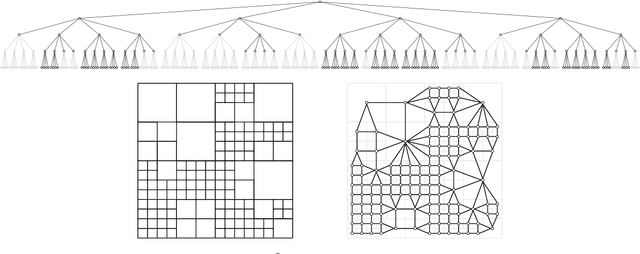
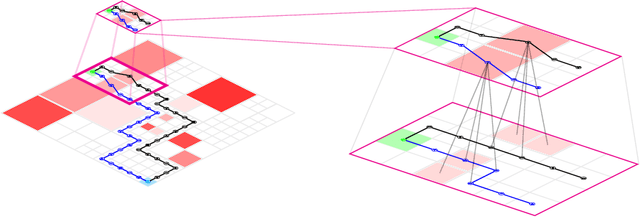
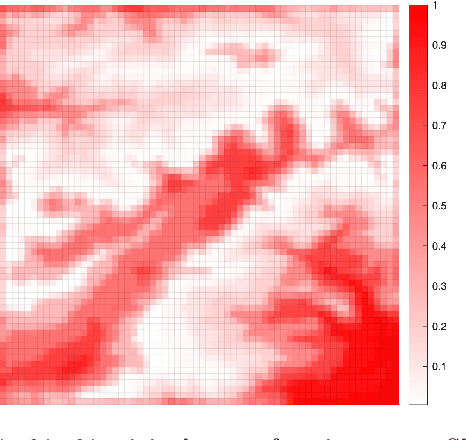
In this paper, we develop a framework for path-planning on abstractions that are not provided to the system a-priori but instead emerge as a function of the agent's available computational resources. We show how a path-planning problem in an environment can be systematically approximated by solving a sequence of easier to solve problems on abstractions of the original space. The properties of the problem are analyzed, and supporting theoretical results presented and discussed. A numerical example is presented to show the utility of the approach and to corroborate the theoretical findings. We conclude by providing a discussion of the results and their interpretation relating to anytime algorithms and bounded rationality.

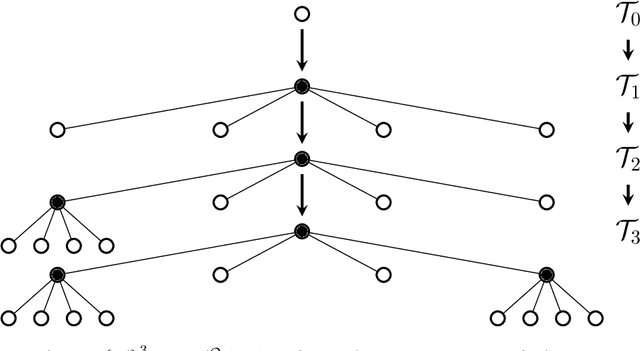
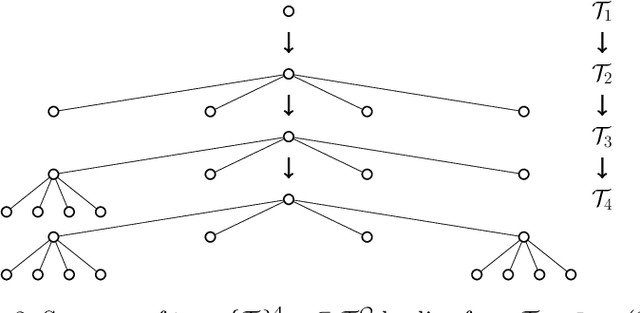
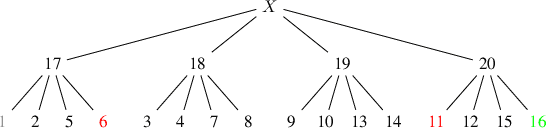
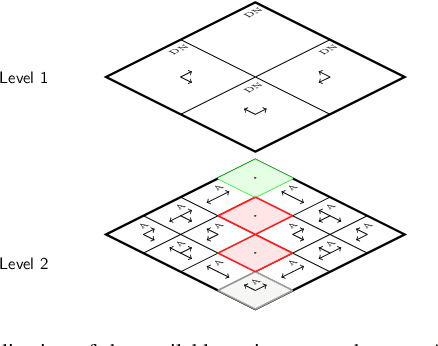
Q-Search Trees: An Information-Theoretic Approach Towards Hierarchical Abstractions for Agents with Computational Limitations

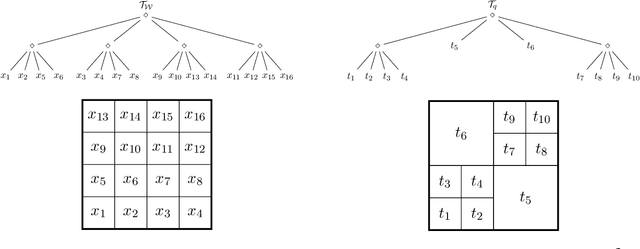
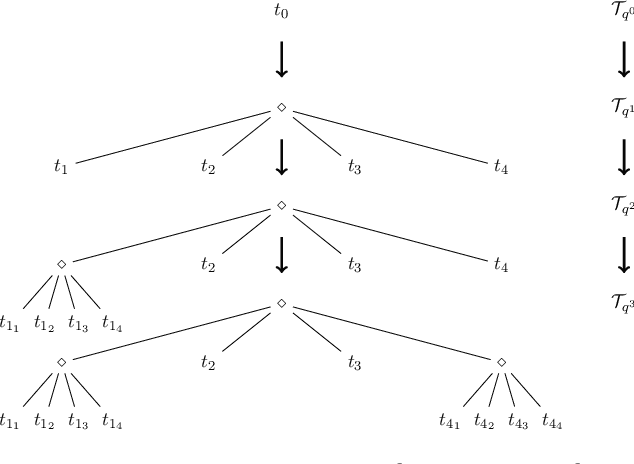
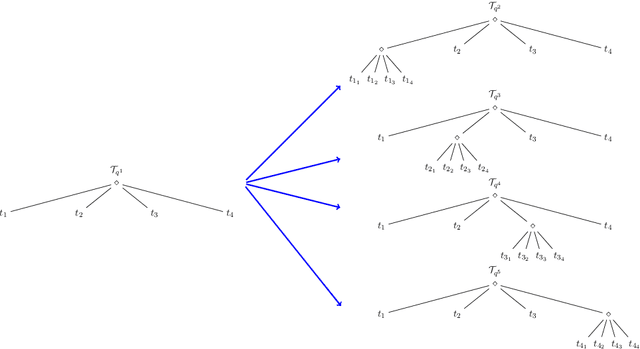
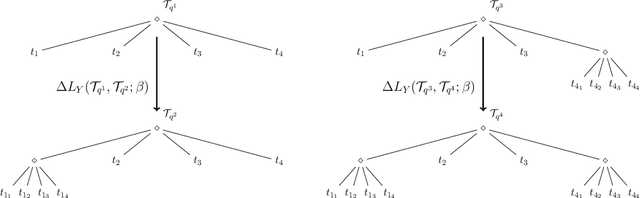
In this paper, we develop a framework to obtain graph abstractions for decision-making by an agent where the abstractions emerge as a function of the agent's limited computational resources. We discuss the connection of the proposed approach with information-theoretic signal compression, and formulate a novel optimization problem to obtain tree-based abstractions as a function of the agent's computational resources. The structural properties of the new problem are discussed in detail, and two algorithmic approaches are proposed to obtain solutions to this optimization problem. We discuss the quality of, and prove relationships between, solutions obtained by the two proposed algorithms. The framework is demonstrated to generate a hierarchy of abstractions for a non-trivial environment.

Hierarchical State Abstractions for Decision-Making Problems with Computational Constraints

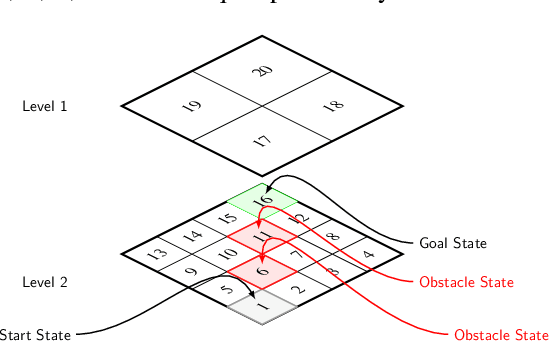
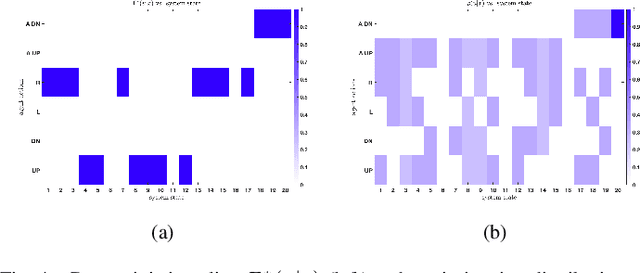
In this semi-tutorial paper, we first review the information-theoretic approach to account for the computational costs incurred during the search for optimal actions in a sequential decision-making problem. The traditional (MDP) framework ignores computational limitations while searching for optimal policies, essentially assuming that the acting agent is perfectly rational and aims for exact optimality. Using the free-energy, a variational principle is introduced that accounts not only for the value of a policy alone, but also considers the cost of finding this optimal policy. The solution of the variational equations arising from this formulation can be obtained using familiar Bellman-like value iterations from dynamic programming (DP) and the Blahut-Arimoto (BA) algorithm from rate distortion theory. Finally, we demonstrate the utility of the approach for generating hierarchies of state abstractions that can be used to best exploit the available computational resources. A numerical example showcases these concepts for a path-planning problem in a grid world environment.