An Information-Theoretic Approach for Path Planning in Agents with Computational Constraints
Paper and Code
May 19, 2020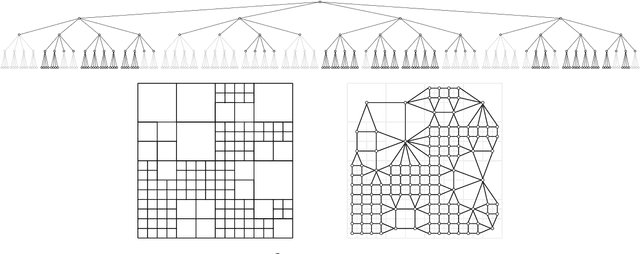
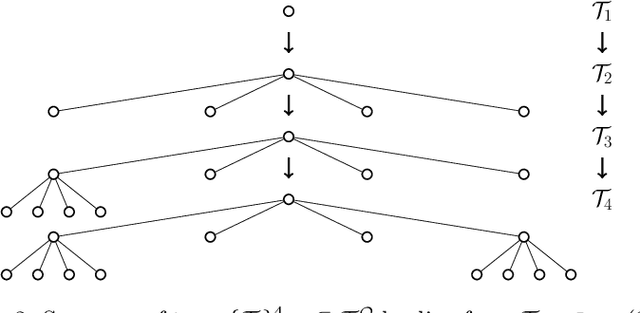
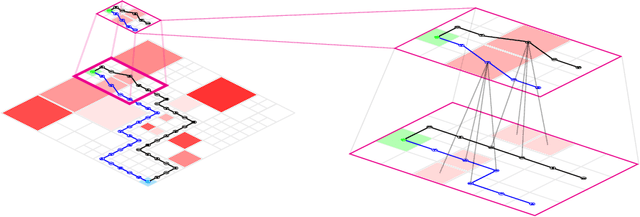
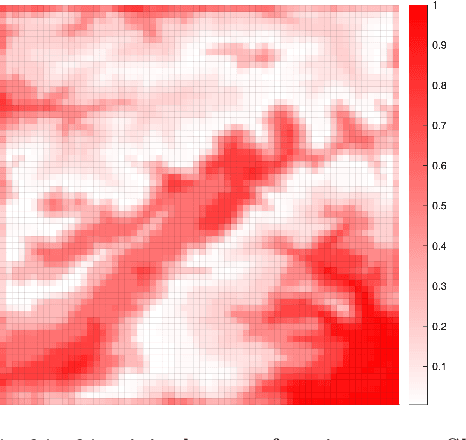
In this paper, we develop a framework for path-planning on abstractions that are not provided to the system a-priori but instead emerge as a function of the agent's available computational resources. We show how a path-planning problem in an environment can be systematically approximated by solving a sequence of easier to solve problems on abstractions of the original space. The properties of the problem are analyzed, and supporting theoretical results presented and discussed. A numerical example is presented to show the utility of the approach and to corroborate the theoretical findings. We conclude by providing a discussion of the results and their interpretation relating to anytime algorithms and bounded rationality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge