Hierarchical State Abstractions for Decision-Making Problems with Computational Constraints
Paper and Code
Oct 22, 2017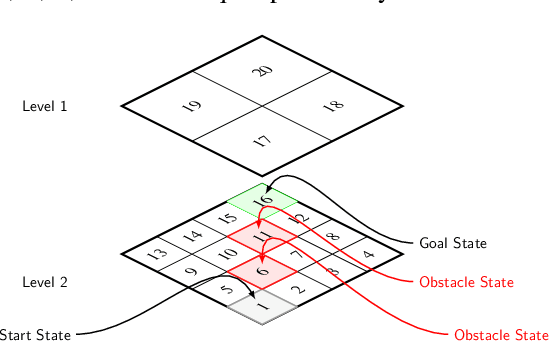
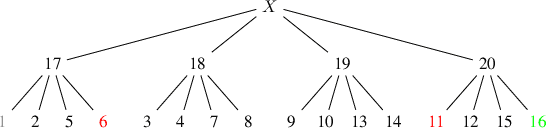
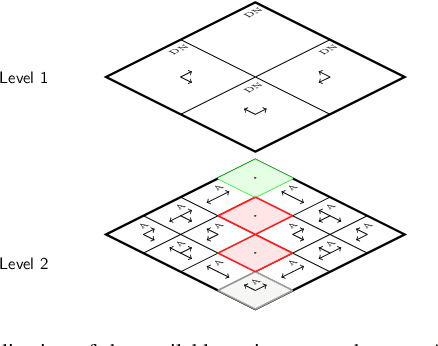
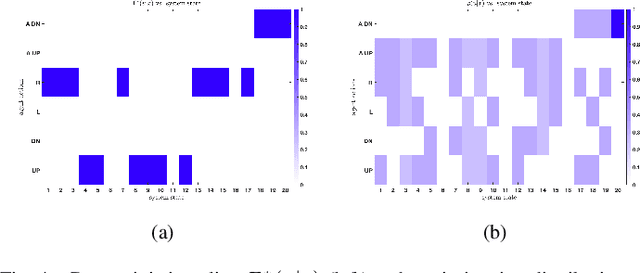
In this semi-tutorial paper, we first review the information-theoretic approach to account for the computational costs incurred during the search for optimal actions in a sequential decision-making problem. The traditional (MDP) framework ignores computational limitations while searching for optimal policies, essentially assuming that the acting agent is perfectly rational and aims for exact optimality. Using the free-energy, a variational principle is introduced that accounts not only for the value of a policy alone, but also considers the cost of finding this optimal policy. The solution of the variational equations arising from this formulation can be obtained using familiar Bellman-like value iterations from dynamic programming (DP) and the Blahut-Arimoto (BA) algorithm from rate distortion theory. Finally, we demonstrate the utility of the approach for generating hierarchies of state abstractions that can be used to best exploit the available computational resources. A numerical example showcases these concepts for a path-planning problem in a grid world environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge