A Linear Programming Approach for Resource-Aware Information-Theoretic Tree Abstractions
Paper and Code
Aug 08, 2022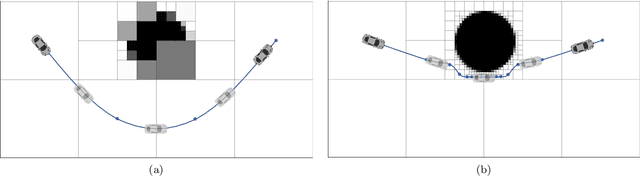
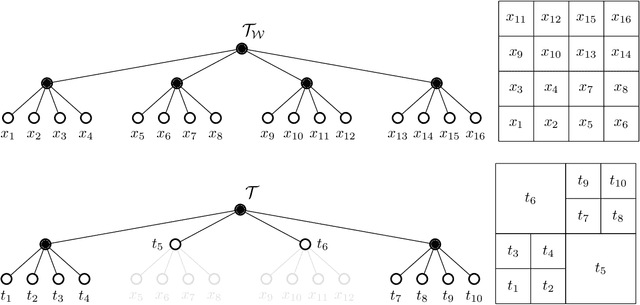
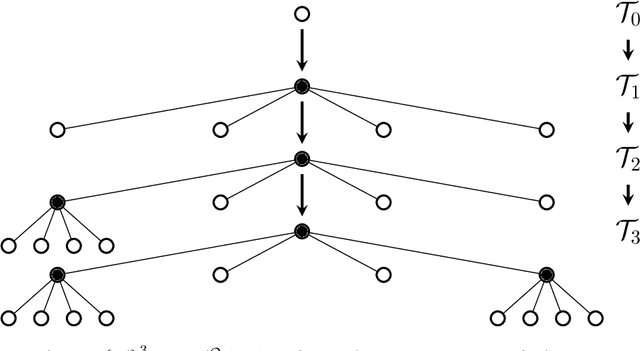
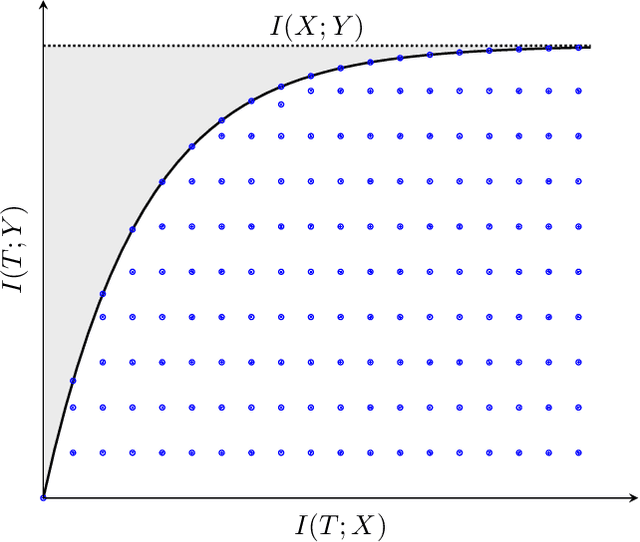
In this chapter, an integer linear programming formulation for the problem of obtaining task-relevant, multi-resolution, environment abstractions for resource-constrained autonomous agents is presented. The formulation leverages concepts from information-theoretic signal compression, specifically, the information bottleneck (IB) method, to pose an abstraction problem as an optimal encoder search over the space of multi-resolution trees. The abstractions emerge in a task-relevant manner as a function of agent information-processing constraints. We detail our formulation, and show how hierarchical tree structures, signal encoders, and information-theoretic methods for signal compression can be unified under a common theme. A discussion delineating the benefits and drawbacks of our formulation is presented, as well as a detailed explanation how our approach can be interpreted within the context of generating abstractions for resource-constrained autonomous systems. It is shown that the resulting information-theoretic abstraction problem over the space of multi-resolution trees can be formulated as a integer linear programming (ILP) problem. We demonstrate the approach on a number of examples, and provide a discussion detailing the differences of the proposed framework compared to existing methods. Lastly, we consider a linear program relaxation of the ILP problem, thereby demonstrating that multi-resolution information-theoretic tree abstractions can be obtained by solving a convex program.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge