Towards Demystifying the Generalization Behaviors When Neural Collapse Emerges

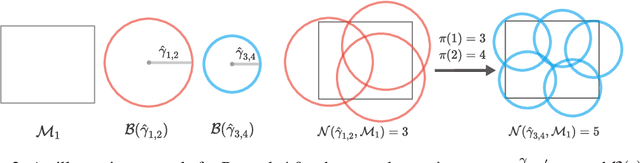
Neural Collapse (NC) is a well-known phenomenon of deep neural networks in the terminal phase of training (TPT). It is characterized by the collapse of features and classifier into a symmetrical structure, known as simplex equiangular tight frame (ETF). While there have been extensive studies on optimization characteristics showing the global optimality of neural collapse, little research has been done on the generalization behaviors during the occurrence of NC. Particularly, the important phenomenon of generalization improvement during TPT has been remaining in an empirical observation and lacking rigorous theoretical explanation. In this paper, we establish the connection between the minimization of CE and a multi-class SVM during TPT, and then derive a multi-class margin generalization bound, which provides a theoretical explanation for why continuing training can still lead to accuracy improvement on test set, even after the train accuracy has reached 100%. Additionally, our further theoretical results indicate that different alignment between labels and features in a simplex ETF can result in varying degrees of generalization improvement, despite all models reaching NC and demonstrating similar optimization performance on train set. We refer to this newly discovered property as "non-conservative generalization". In experiments, we also provide empirical observations to verify the indications suggested by our theoretical results.

A Study of Neural Collapse Phenomenon: Grassmannian Frame, Symmetry, Generalization

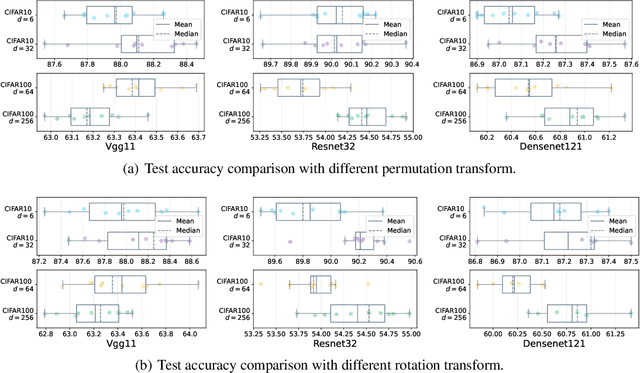
In this paper, we extends original Neural Collapse Phenomenon by proving Generalized Neural Collapse hypothesis. We obtain Grassmannian Frame structure from the optimization and generalization of classification. This structure maximally separates features of every two classes on a sphere and does not require a larger feature dimension than the number of classes. Out of curiosity about the symmetry of Grassmannian Frame, we conduct experiments to explore if models with different Grassmannian Frames have different performance. As a result, we discover the Symmetric Generalization phenomenon. We provide a theorem to explain Symmetric Generalization of permutation. However, the question of why different directions of features can lead to such different generalization is still open for future investigation.

Asymptotically Unbiased Instance-wise Regularized Partial AUC Optimization: Theory and Algorithm

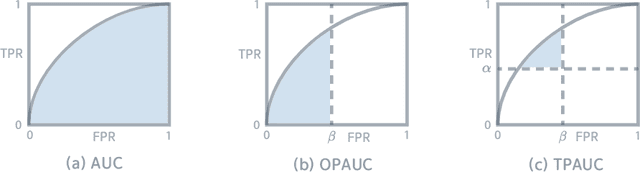
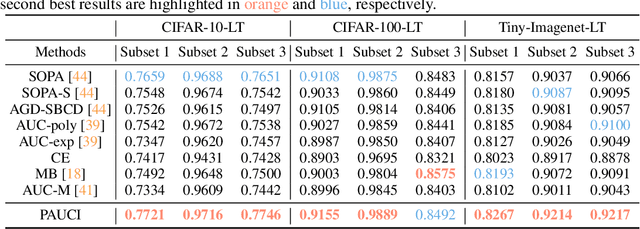
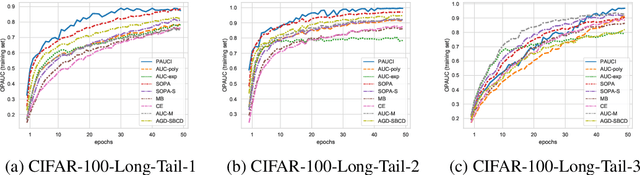
The Partial Area Under the ROC Curve (PAUC), typically including One-way Partial AUC (OPAUC) and Two-way Partial AUC (TPAUC), measures the average performance of a binary classifier within a specific false positive rate and/or true positive rate interval, which is a widely adopted measure when decision constraints must be considered. Consequently, PAUC optimization has naturally attracted increasing attention in the machine learning community within the last few years. Nonetheless, most of the existing methods could only optimize PAUC approximately, leading to inevitable biases that are not controllable. Fortunately, a recent work presents an unbiased formulation of the PAUC optimization problem via distributional robust optimization. However, it is based on the pair-wise formulation of AUC, which suffers from the limited scalability w.r.t. sample size and a slow convergence rate, especially for TPAUC. To address this issue, we present a simpler reformulation of the problem in an asymptotically unbiased and instance-wise manner. For both OPAUC and TPAUC, we come to a nonconvex strongly concave minimax regularized problem of instance-wise functions. On top of this, we employ an efficient solver enjoys a linear per-iteration computational complexity w.r.t. the sample size and a time-complexity of $O(\epsilon^{-1/3})$ to reach a $\epsilon$ stationary point. Furthermore, we find that the minimax reformulation also facilitates the theoretical analysis of generalization error as a byproduct. Compared with the existing results, we present new error bounds that are much easier to prove and could deal with hypotheses with real-valued outputs. Finally, extensive experiments on several benchmark datasets demonstrate the effectiveness of our method.