Asymptotically Unbiased Instance-wise Regularized Partial AUC Optimization: Theory and Algorithm
Paper and Code
Oct 11, 2022
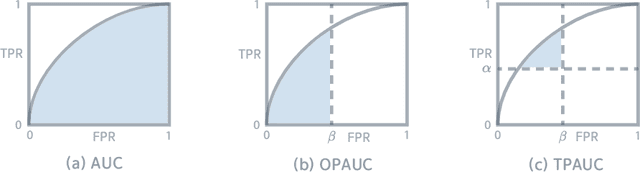
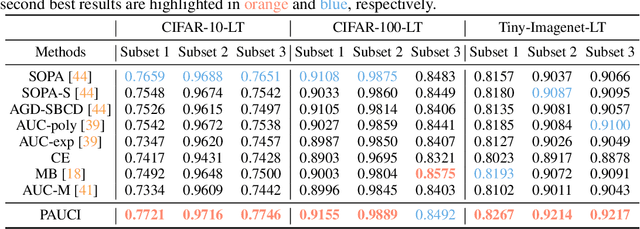
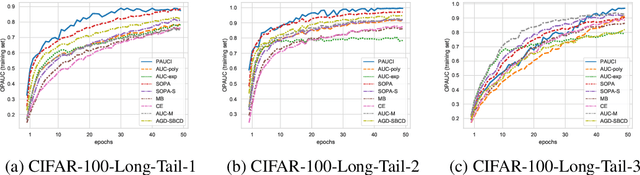
The Partial Area Under the ROC Curve (PAUC), typically including One-way Partial AUC (OPAUC) and Two-way Partial AUC (TPAUC), measures the average performance of a binary classifier within a specific false positive rate and/or true positive rate interval, which is a widely adopted measure when decision constraints must be considered. Consequently, PAUC optimization has naturally attracted increasing attention in the machine learning community within the last few years. Nonetheless, most of the existing methods could only optimize PAUC approximately, leading to inevitable biases that are not controllable. Fortunately, a recent work presents an unbiased formulation of the PAUC optimization problem via distributional robust optimization. However, it is based on the pair-wise formulation of AUC, which suffers from the limited scalability w.r.t. sample size and a slow convergence rate, especially for TPAUC. To address this issue, we present a simpler reformulation of the problem in an asymptotically unbiased and instance-wise manner. For both OPAUC and TPAUC, we come to a nonconvex strongly concave minimax regularized problem of instance-wise functions. On top of this, we employ an efficient solver enjoys a linear per-iteration computational complexity w.r.t. the sample size and a time-complexity of $O(\epsilon^{-1/3})$ to reach a $\epsilon$ stationary point. Furthermore, we find that the minimax reformulation also facilitates the theoretical analysis of generalization error as a byproduct. Compared with the existing results, we present new error bounds that are much easier to prove and could deal with hypotheses with real-valued outputs. Finally, extensive experiments on several benchmark datasets demonstrate the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge