Gradient Descent Robustly Learns the Intrinsic Dimension of Data in Training Convolutional Neural Networks

Modern neural networks are usually highly over-parameterized. Behind the wide usage of over-parameterized networks is the belief that, if the data are simple, then the trained network will be automatically equivalent to a simple predictor. Following this intuition, many existing works have studied different notions of "ranks" of neural networks and their relation to the rank of data. In this work, we study the rank of convolutional neural networks (CNNs) trained by gradient descent, with a specific focus on the robustness of the rank to image background noises. Specifically, we point out that, when adding background noises to images, the rank of the CNN trained with gradient descent is affected far less compared with the rank of the data. We support our claim with a theoretical case study, where we consider a particular data model to characterize low-rank clean images with added background noises. We prove that CNNs trained by gradient descent can learn the intrinsic dimension of clean images, despite the presence of relatively large background noises. We also conduct experiments on synthetic and real datasets to further validate our claim.

Towards Demystifying the Generalization Behaviors When Neural Collapse Emerges

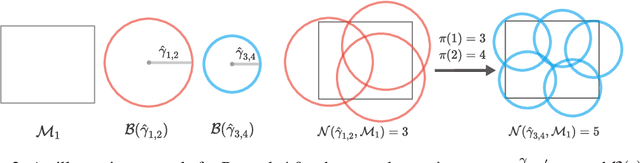
Neural Collapse (NC) is a well-known phenomenon of deep neural networks in the terminal phase of training (TPT). It is characterized by the collapse of features and classifier into a symmetrical structure, known as simplex equiangular tight frame (ETF). While there have been extensive studies on optimization characteristics showing the global optimality of neural collapse, little research has been done on the generalization behaviors during the occurrence of NC. Particularly, the important phenomenon of generalization improvement during TPT has been remaining in an empirical observation and lacking rigorous theoretical explanation. In this paper, we establish the connection between the minimization of CE and a multi-class SVM during TPT, and then derive a multi-class margin generalization bound, which provides a theoretical explanation for why continuing training can still lead to accuracy improvement on test set, even after the train accuracy has reached 100%. Additionally, our further theoretical results indicate that different alignment between labels and features in a simplex ETF can result in varying degrees of generalization improvement, despite all models reaching NC and demonstrating similar optimization performance on train set. We refer to this newly discovered property as "non-conservative generalization". In experiments, we also provide empirical observations to verify the indications suggested by our theoretical results.

A Study of Neural Collapse Phenomenon: Grassmannian Frame, Symmetry, Generalization

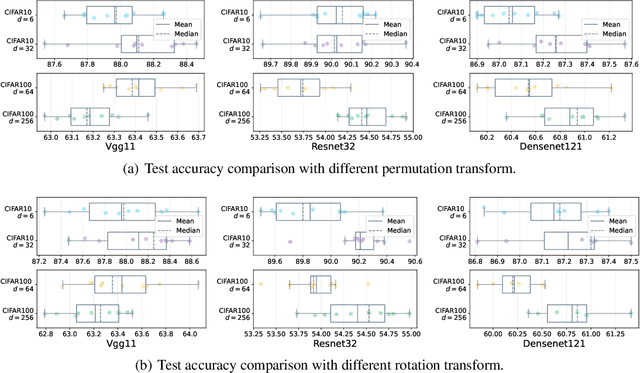
In this paper, we extends original Neural Collapse Phenomenon by proving Generalized Neural Collapse hypothesis. We obtain Grassmannian Frame structure from the optimization and generalization of classification. This structure maximally separates features of every two classes on a sphere and does not require a larger feature dimension than the number of classes. Out of curiosity about the symmetry of Grassmannian Frame, we conduct experiments to explore if models with different Grassmannian Frames have different performance. As a result, we discover the Symmetric Generalization phenomenon. We provide a theorem to explain Symmetric Generalization of permutation. However, the question of why different directions of features can lead to such different generalization is still open for future investigation.