Learning Interpretable Models for Coupled Networks Under Domain Constraints

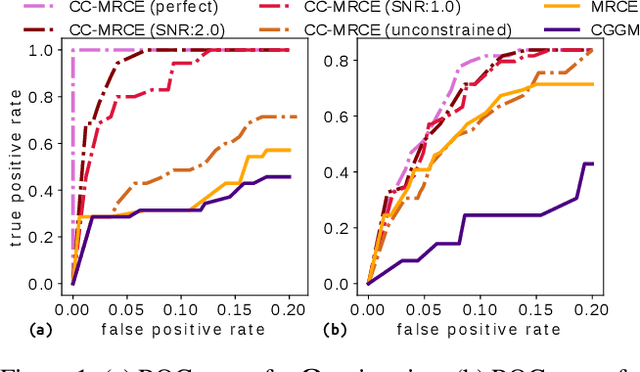
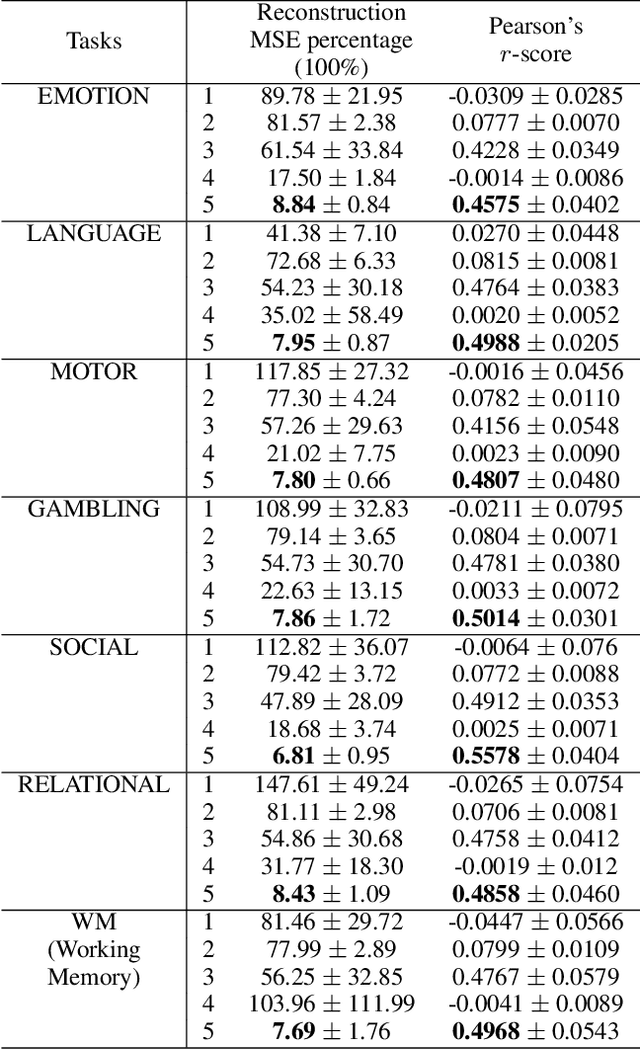
Modeling the behavior of coupled networks is challenging due to their intricate dynamics. For example in neuroscience, it is of critical importance to understand the relationship between the functional neural processes and anatomical connectivities. Modern neuroimaging techniques allow us to separately measure functional connectivity through fMRI imaging and the underlying white matter wiring through diffusion imaging. Previous studies have shown that structural edges in brain networks improve the inference of functional edges and vice versa. In this paper, we investigate the idea of coupled networks through an optimization framework by focusing on interactions between structural edges and functional edges of brain networks. We consider both types of edges as observed instances of random variables that represent different underlying network processes. The proposed framework does not depend on Gaussian assumptions and achieves a more robust performance on general data compared with existing approaches. To incorporate existing domain knowledge into such studies, we propose a novel formulation to place hard network constraints on the noise term while estimating interactions. This not only leads to a cleaner way of applying network constraints but also provides a more scalable solution when network connectivity is sparse. We validate our method on multishell diffusion and task-evoked fMRI datasets from the Human Connectome Project, leading to both important insights on structural backbones that support various types of task activities as well as general solutions to the study of coupled networks.

DANR: Discrepancy-aware Network Regularization

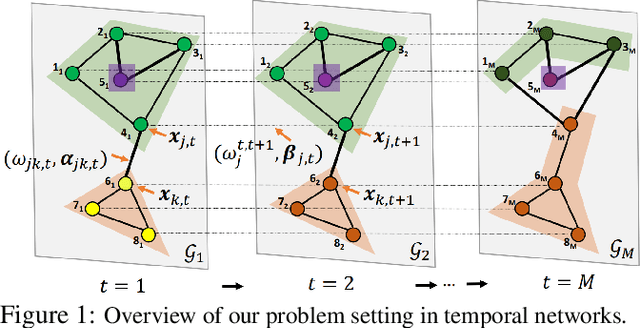
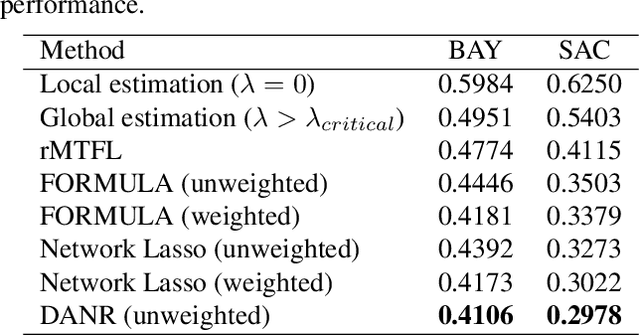
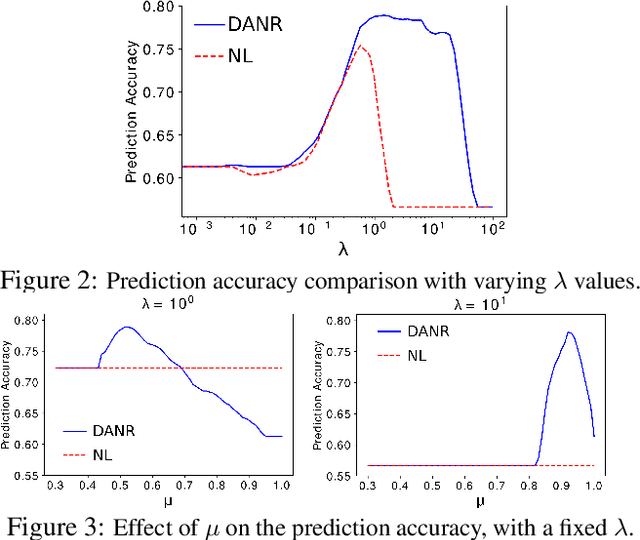
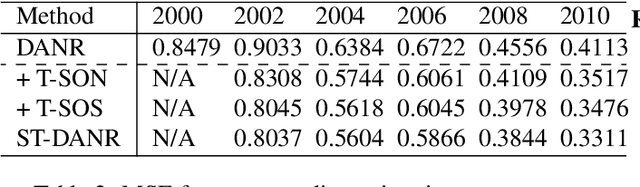
Network regularization is an effective tool for incorporating structural prior knowledge to learn coherent models over networks, and has yielded provably accurate estimates in applications ranging from spatial economics to neuroimaging studies. Recently, there has been an increasing interest in extending network regularization to the spatio-temporal case to accommodate the evolution of networks. However, in both static and spatio-temporal cases, missing or corrupted edge weights can compromise the ability of network regularization to discover desired solutions. To address these gaps, we propose a novel approach---{\it discrepancy-aware network regularization} (DANR)---that is robust to inadequate regularizations and effectively captures model evolution and structural changes over spatio-temporal networks. We develop a distributed and scalable algorithm based on the alternating direction method of multipliers (ADMM) to solve the proposed problem with guaranteed convergence to global optimum solutions. Experimental results on both synthetic and real-world networks demonstrate that our approach achieves improved performance on various tasks, and enables interpretation of model changes in evolving networks.

Autism Classification Using Brain Functional Connectivity Dynamics and Machine Learning

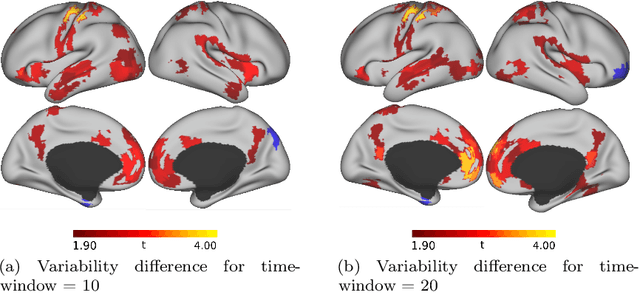
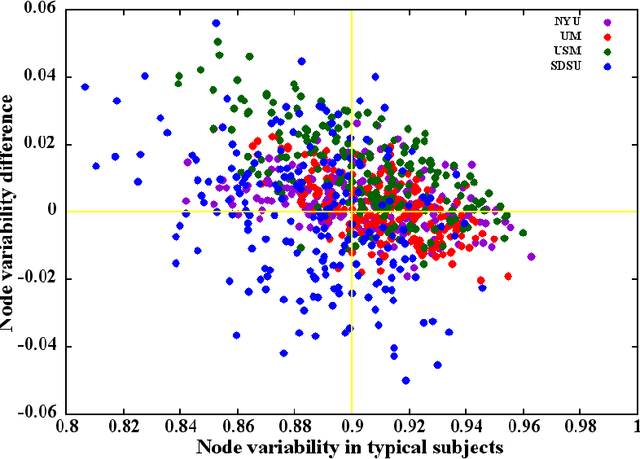
The goal of the present study is to identify autism using machine learning techniques and resting-state brain imaging data, leveraging the temporal variability of the functional connections (FC) as the only information. We estimated and compared the FC variability across brain regions between typical, healthy subjects and autistic population by analyzing brain imaging data from a world-wide multi-site database known as ABIDE (Autism Brain Imaging Data Exchange). Our analysis revealed that patients diagnosed with autism spectrum disorder (ASD) show increased FC variability in several brain regions that are associated with low FC variability in the typical brain. We then used the enhanced FC variability of brain regions as features for training machine learning models for ASD classification and achieved 65% accuracy in identification of ASD versus control subjects within the dataset. We also used node strength estimated from number of functional connections per node averaged over the whole scan as features for ASD classification.The results reveal that the dynamic FC measures outperform or are comparable with the static FC measures in predicting ASD.

Discriminative Subnetworks with Regularized Spectral Learning for Global-state Network Data

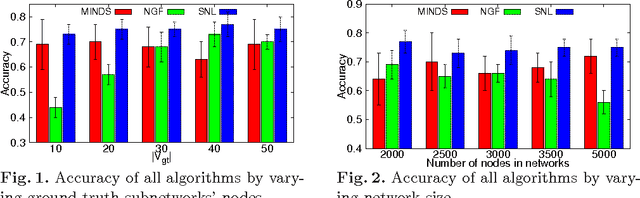
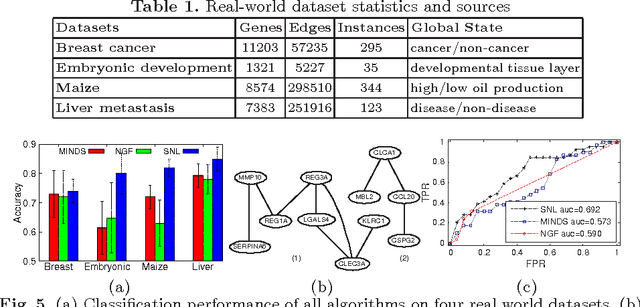
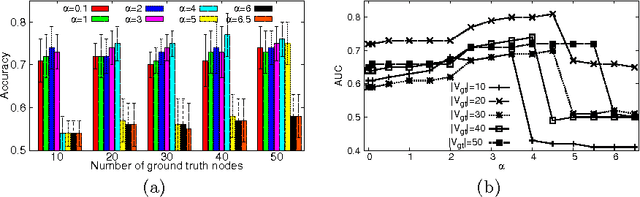
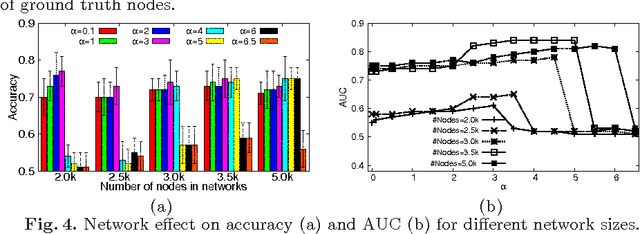
Data mining practitioners are facing challenges from data with network structure. In this paper, we address a specific class of global-state networks which comprises of a set of network instances sharing a similar structure yet having different values at local nodes. Each instance is associated with a global state which indicates the occurrence of an event. The objective is to uncover a small set of discriminative subnetworks that can optimally classify global network values. Unlike most existing studies which explore an exponential subnetwork space, we address this difficult problem by adopting a space transformation approach. Specifically, we present an algorithm that optimizes a constrained dual-objective function to learn a low-dimensional subspace that is capable of discriminating networks labelled by different global states, while reconciling with common network topology sharing across instances. Our algorithm takes an appealing approach from spectral graph learning and we show that the globally optimum solution can be achieved via matrix eigen-decomposition.