Discriminative Subnetworks with Regularized Spectral Learning for Global-state Network Data
Paper and Code
Dec 19, 2015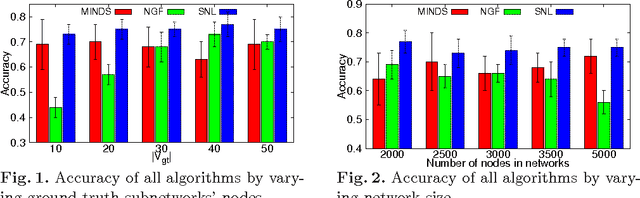
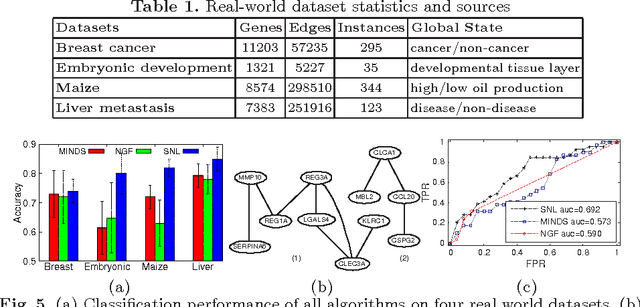
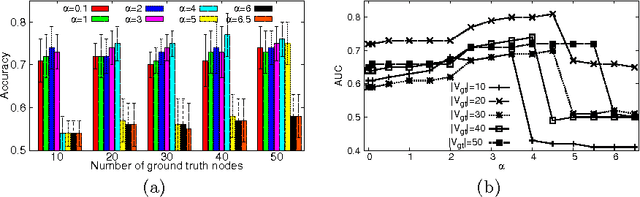
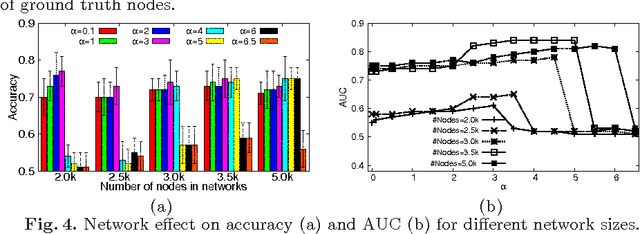
Data mining practitioners are facing challenges from data with network structure. In this paper, we address a specific class of global-state networks which comprises of a set of network instances sharing a similar structure yet having different values at local nodes. Each instance is associated with a global state which indicates the occurrence of an event. The objective is to uncover a small set of discriminative subnetworks that can optimally classify global network values. Unlike most existing studies which explore an exponential subnetwork space, we address this difficult problem by adopting a space transformation approach. Specifically, we present an algorithm that optimizes a constrained dual-objective function to learn a low-dimensional subspace that is capable of discriminating networks labelled by different global states, while reconciling with common network topology sharing across instances. Our algorithm takes an appealing approach from spectral graph learning and we show that the globally optimum solution can be achieved via matrix eigen-decomposition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge