DANR: Discrepancy-aware Network Regularization
Paper and Code
May 31, 2020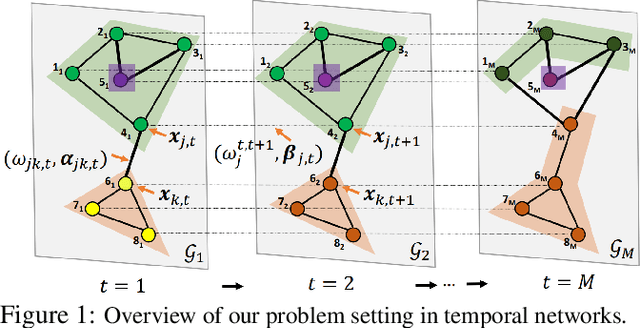
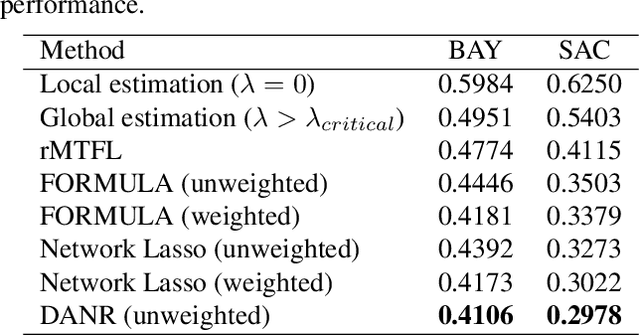
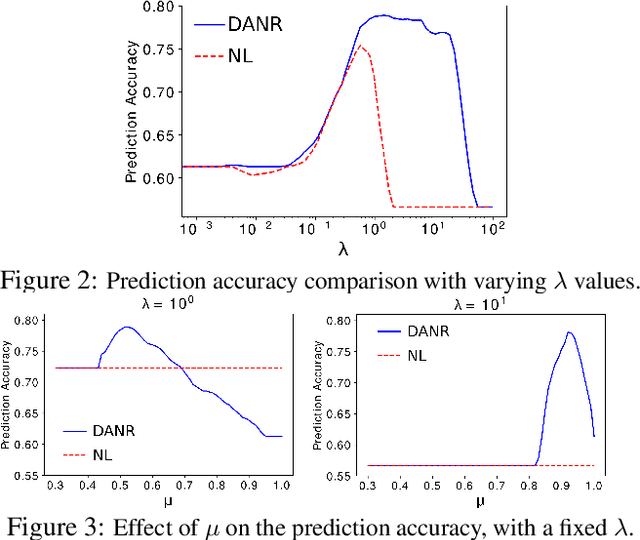
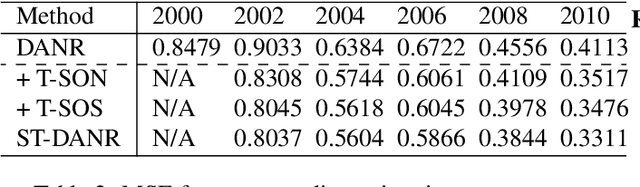
Network regularization is an effective tool for incorporating structural prior knowledge to learn coherent models over networks, and has yielded provably accurate estimates in applications ranging from spatial economics to neuroimaging studies. Recently, there has been an increasing interest in extending network regularization to the spatio-temporal case to accommodate the evolution of networks. However, in both static and spatio-temporal cases, missing or corrupted edge weights can compromise the ability of network regularization to discover desired solutions. To address these gaps, we propose a novel approach---{\it discrepancy-aware network regularization} (DANR)---that is robust to inadequate regularizations and effectively captures model evolution and structural changes over spatio-temporal networks. We develop a distributed and scalable algorithm based on the alternating direction method of multipliers (ADMM) to solve the proposed problem with guaranteed convergence to global optimum solutions. Experimental results on both synthetic and real-world networks demonstrate that our approach achieves improved performance on various tasks, and enables interpretation of model changes in evolving networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge