Learning Interpretable Models for Coupled Networks Under Domain Constraints

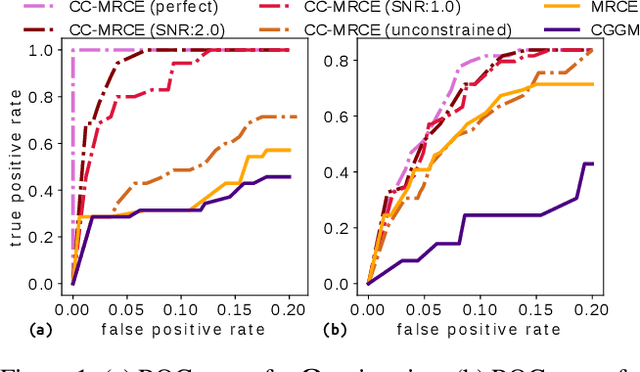
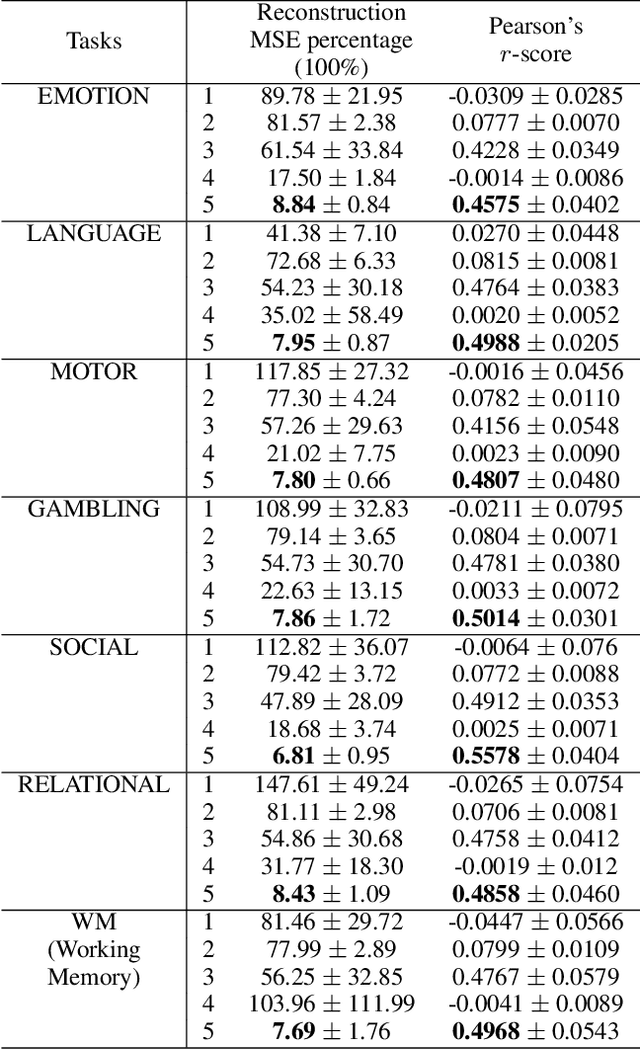
Modeling the behavior of coupled networks is challenging due to their intricate dynamics. For example in neuroscience, it is of critical importance to understand the relationship between the functional neural processes and anatomical connectivities. Modern neuroimaging techniques allow us to separately measure functional connectivity through fMRI imaging and the underlying white matter wiring through diffusion imaging. Previous studies have shown that structural edges in brain networks improve the inference of functional edges and vice versa. In this paper, we investigate the idea of coupled networks through an optimization framework by focusing on interactions between structural edges and functional edges of brain networks. We consider both types of edges as observed instances of random variables that represent different underlying network processes. The proposed framework does not depend on Gaussian assumptions and achieves a more robust performance on general data compared with existing approaches. To incorporate existing domain knowledge into such studies, we propose a novel formulation to place hard network constraints on the noise term while estimating interactions. This not only leads to a cleaner way of applying network constraints but also provides a more scalable solution when network connectivity is sparse. We validate our method on multishell diffusion and task-evoked fMRI datasets from the Human Connectome Project, leading to both important insights on structural backbones that support various types of task activities as well as general solutions to the study of coupled networks.