A Combined Deep Learning based End-to-End Video Coding Architecture for YUV Color Space

Most of the existing deep learning based end-to-end video coding (DLEC) architectures are designed specifically for RGB color format, yet the video coding standards, including H.264/AVC, H.265/HEVC and H.266/VVC developed over past few decades, have been designed primarily for YUV 4:2:0 format, where the chrominance (U and V) components are subsampled to achieve superior compression performances considering the human visual system. While a broad number of papers on DLEC compare these two distinct coding schemes in RGB domain, it is ideal to have a common evaluation framework in YUV 4:2:0 domain for a more fair comparison. This paper introduces a new DLEC architecture for video coding to effectively support YUV 4:2:0 and compares its performance against the HEVC standard under a common evaluation framework. The experimental results on YUV 4:2:0 video sequences show that the proposed architecture can outperform HEVC in intra-frame coding, however inter-frame coding is not as efficient on contrary to the RGB coding results reported in recent papers.

Transform Network Architectures for Deep Learning based End-to-End Image/Video Coding in Subsampled Color Spaces

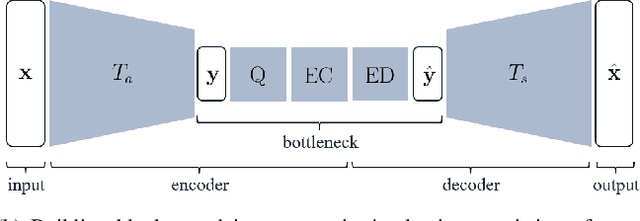
Most of the existing deep learning based end-to-end image/video coding (DLEC) architectures are designed for non-subsampled RGB color format. However, in order to achieve a superior coding performance, many state-of-the-art block-based compression standards such as High Efficiency Video Coding (HEVC/H.265) and Versatile Video Coding (VVC/H.266) are designed primarily for YUV 4:2:0 format, where U and V components are subsampled by considering the human visual system. This paper investigates various DLEC designs to support YUV 4:2:0 format by comparing their performance against the main profiles of HEVC and VVC standards under a common evaluation framework. Moreover, a new transform network architecture is proposed to improve the efficiency of coding YUV 4:2:0 data. The experimental results on YUV 4:2:0 datasets show that the proposed architecture significantly outperforms naive extensions of existing architectures designed for RGB format and achieves about 10% average BD-rate improvement over the intra-frame coding in HEVC.

Parametric Graph-based Separable Transforms for Video Coding

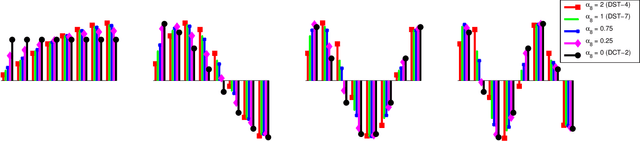
In many video coding systems, separable transforms (such as two-dimensional DCT-2) have been used to code block residual signals obtained after prediction. This paper proposes a parametric approach to build graph-based separable transforms (GBSTs) for video coding. Specifically, a GBST is derived from a pair of line graphs, whose weights are determined based on two non-negative parameters. As certain choices of those parameters correspond to the discrete sine and cosine transform types used in recent video coding standards (including DCT-2, DST-7 and DCT-8), this paper further optimizes these graph parameters to better capture residual block statistics and improve video coding efficiency. The proposed GBSTs are tested on the Versatile Video Coding (VVC) reference software, and the experimental results show that about 0.4\% average coding gain is achieved over the existing set of separable transforms constructed based on DCT-2, DST-7 and DCT-8 in VVC.

Graph-based Transforms for Video Coding

In many state-of-the-art compression systems, signal transformation is an integral part of the encoding and decoding process, where transforms provide compact representations for the signals of interest. This paper introduces a class of transforms called graph-based transforms (GBTs) for video compression, and proposes two different techniques to design GBTs. In the first technique, we formulate an optimization problem to learn graphs from data and provide solutions for optimal separable and nonseparable GBT designs, called GL-GBTs. The optimality of the proposed GL-GBTs is also theoretically analyzed based on Gaussian-Markov random field (GMRF) models for intra and inter predicted block signals. The second technique develops edge-adaptive GBTs (EA-GBTs) in order to flexibly adapt transforms to block signals with image edges (discontinuities). The advantages of EA-GBTs are both theoretically and empirically demonstrated. Our experimental results demonstrate that the proposed transforms can significantly outperform the traditional Karhunen-Loeve transform (KLT).

Graph Learning from Filtered Signals: Graph System and Diffusion Kernel Identification

This paper introduces a novel graph signal processing framework for building graph-based models from classes of filtered signals. In our framework, graph-based modeling is formulated as a graph system identification problem, where the goal is to learn a weighted graph (a graph Laplacian matrix) and a graph-based filter (a function of graph Laplacian matrices). In order to solve the proposed problem, an algorithm is developed to jointly identify a graph and a graph-based filter (GBF) from multiple signal/data observations. Our algorithm is valid under the assumption that GBFs are one-to-one functions. The proposed approach can be applied to learn diffusion (heat) kernels, which are popular in various fields for modeling diffusion processes. In addition, for specific choices of graph-based filters, the proposed problem reduces to a graph Laplacian estimation problem. Our experimental results demonstrate that the proposed algorithm outperforms the current state-of-the-art methods. We also implement our framework on a real climate dataset for modeling of temperature signals.

Learning Graphs with Monotone Topology Properties and Multiple Connected Components

Recent papers have formulated the problem of learning graphs from data as an inverse covariance estimation with graph Laplacian constraints. While such problems are convex, existing methods cannot guarantee that solutions will have specific graph topology properties (e.g., being $k$-partite), which are desirable for some applications. In fact, the problem of learning a graph with given topology properties, e.g., finding the $k$-partite graph that best matches the data, is in general non-convex. In this paper, we develop novel theoretical results that provide performance guarantees for an approach to solve these problems. Our solution decomposes this problem into two sub-problems, for which efficient solutions are known. Specifically, a graph topology inference (GTI) step is employed to select a feasible graph topology, i.e., one having the desired property. Then, a graph weight estimation (GWE) step is performed by solving a generalized graph Laplacian estimation problem, where edges are constrained by the topology found in the GTI step. Our main result is a bound on the error of the GWE step as a function of the error in the GTI step. This error bound indicates that the GTI step should be solved using an algorithm that approximates the similarity matrix by another matrix whose entries have been thresholded to zero to have the desired type of graph topology. The GTI stage can leverage existing methods (e.g., state of the art approaches for graph coloring) which are typically based on minimizing the total weight of removed edges. Since the GWE stage is formulated as an inverse covariance estimation problem with linear constraints, it can be solved using existing convex optimization methods. We demonstrate that our two step approach can achieve good results for both synthetic and texture image data.

Graph Learning from Data under Structural and Laplacian Constraints

Graphs are fundamental mathematical structures used in various fields to represent data, signals and processes. In this paper, we propose a novel framework for learning/estimating graphs from data. The proposed framework includes (i) formulation of various graph learning problems, (ii) their probabilistic interpretations and (iii) associated algorithms. Specifically, graph learning problems are posed as estimation of graph Laplacian matrices from some observed data under given structural constraints (e.g., graph connectivity and sparsity level). From a probabilistic perspective, the problems of interest correspond to maximum a posteriori (MAP) parameter estimation of Gaussian-Markov random field (GMRF) models, whose precision (inverse covariance) is a graph Laplacian matrix. For the proposed graph learning problems, specialized algorithms are developed by incorporating the graph Laplacian and structural constraints. The experimental results demonstrate that the proposed algorithms outperform the current state-of-the-art methods in terms of accuracy and computational efficiency.