Pre-demosaic Graph-based Light Field Image Compression

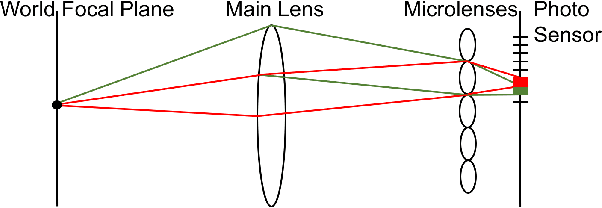
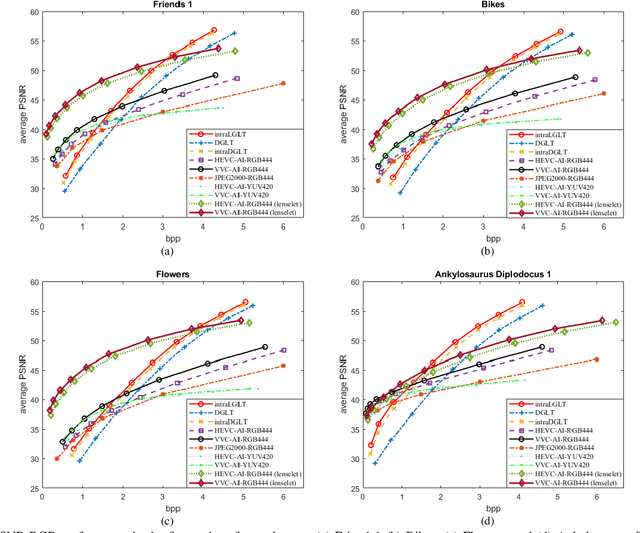
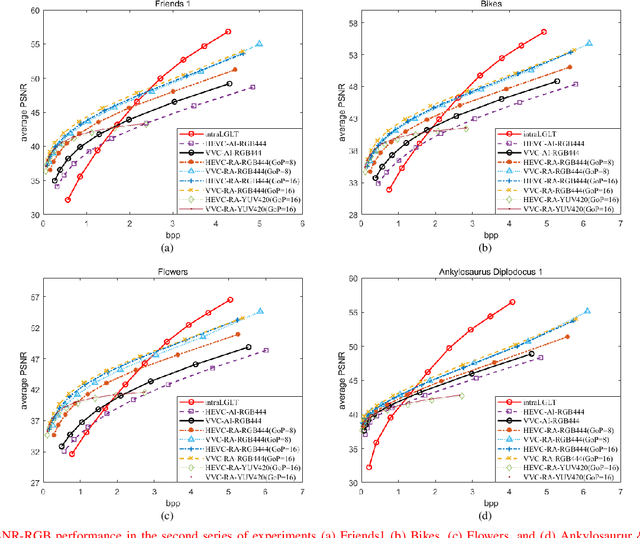
A plenoptic light field (LF) camera places an array of microlenses in front of an image sensor in order to separately capture different directional rays arriving at an image pixel. Using a conventional Bayer pattern, data captured at each pixel is a single color component (R, G or B). The sensed data then undergoes demosaicking (interpolation of RGB components per pixel) and conversion to an array of sub-aperture images (SAIs). In this paper, we propose a new LF image coding scheme based on graph lifting transform (GLT), where the acquired sensor data are coded in the original captured form without pre-processing. Specifically, we directly map raw sensed color data to the SAIs, resulting in sparsely distributed color pixels on 2D grids, and perform demosaicking at the receiver after decoding. To exploit spatial correlation among the sparse pixels, we propose a novel intra-prediction scheme, where the prediction kernel is determined according to the local gradient estimated from already coded neighboring pixel blocks. We then connect the pixels by forming a graph, modeling the prediction residuals statistically as a Gaussian Markov Random Field (GMRF). The optimal edge weights are computed via a graph learning method using a set of training SAIs. The residual data is encoded via low-complexity GLT. Experiments show that at high PSNRs -- important for archiving and instant storage scenarios -- our method outperformed significantly a conventional light field image coding scheme with demosaicking followed by High Efficiency Video Coding (HEVC).

Graph-based Transforms for Video Coding

In many state-of-the-art compression systems, signal transformation is an integral part of the encoding and decoding process, where transforms provide compact representations for the signals of interest. This paper introduces a class of transforms called graph-based transforms (GBTs) for video compression, and proposes two different techniques to design GBTs. In the first technique, we formulate an optimization problem to learn graphs from data and provide solutions for optimal separable and nonseparable GBT designs, called GL-GBTs. The optimality of the proposed GL-GBTs is also theoretically analyzed based on Gaussian-Markov random field (GMRF) models for intra and inter predicted block signals. The second technique develops edge-adaptive GBTs (EA-GBTs) in order to flexibly adapt transforms to block signals with image edges (discontinuities). The advantages of EA-GBTs are both theoretically and empirically demonstrated. Our experimental results demonstrate that the proposed transforms can significantly outperform the traditional Karhunen-Loeve transform (KLT).