Hideaki Ishii
Distributed Parameter Estimation with Gaussian Observation Noises in Time-varying Digraphs
Nov 08, 2023Abstract:In this paper, we consider the problem of distributed parameter estimation in sensor networks. Each sensor makes successive observations of an unknown $d$-dimensional parameter, which might be subject to Gaussian random noises. The sensors aim to infer the true value of the unknown parameter by cooperating with each other. To this end, we first generalize the so-called dynamic regressor extension and mixing (DREM) algorithm to stochastic systems, with which the problem of estimating a $d$-dimensional vector parameter is transformed to that of $d$ scalar ones: one for each of the unknown parameters. For each of the scalar problem, both combine-then-adapt (CTA) and adapt-then-combine (ATC) diffusion-based estimation algorithms are given, where each sensor performs a combination step to fuse the local estimates in its in-neighborhood, alongside an adaptation step to process its streaming observations. Under weak conditions on network topology and excitation of regressors, we show that the proposed estimators guarantee that each sensor infers the true parameter, even if any individual of them cannot by itself. Specifically, it is required that the union of topologies over an interval with fixed length is strongly connected. Moreover, the sensors must collectively satisfy a cooperative persistent excitation (PE) condition, which relaxes the traditional PE condition. Numerical examples are finally provided to illustrate the established results.
Privacy-preserving Distributed Machine Learning via Local Randomization and ADMM Perturbation
Sep 09, 2019
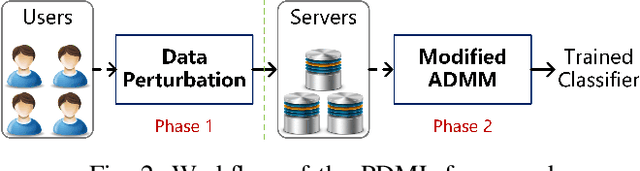
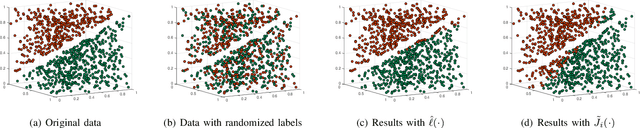
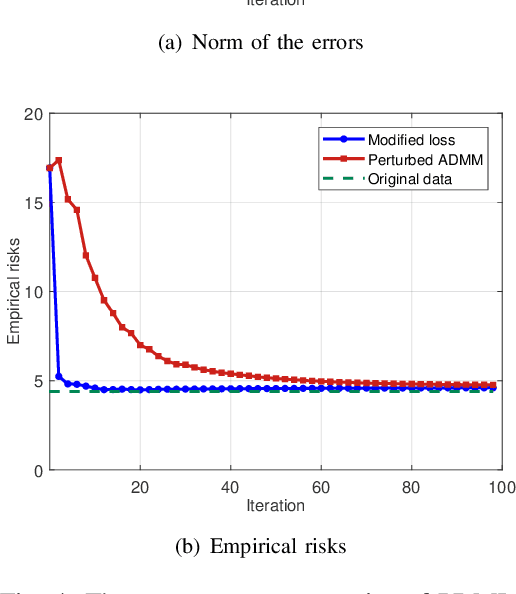
Abstract:With the proliferation of training data, distributed machine learning (DML) is becoming more competent for large-scale learning tasks. However, privacy concerns have to be given priority in DML, since training data may contain sensitive information of users. In this paper, we propose a privacy-preserving ADMM-based DML framework with two novel features: First, we remove the assumption commonly made in the literature that the users trust the server collecting their data. Second, the framework provides heterogeneous privacy for users depending on data's sensitive levels and servers' trust degrees. The challenging issue is to keep the accumulation of privacy losses over ADMM iterations minimal. In the proposed framework, a local randomization approach, which is differentially private, is adopted to provide users with self-controlled privacy guarantee for the most sensitive information. Further, the ADMM algorithm is perturbed through a combined noise-adding method, which simultaneously preserves privacy for users' less sensitive information and strengthens the privacy protection of the most sensitive information. We provide detailed analyses on the performance of the trained model according to its generalization error. Finally, we conduct extensive experiments using real-world datasets to validate the theoretical results and evaluate the classification performance of the proposed framework.
Two-Way Coding and Attack Decoupling in Control Systems Under Injection Attacks
Sep 04, 2019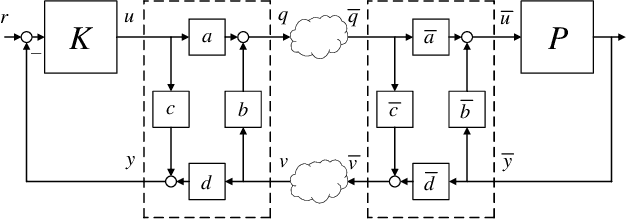
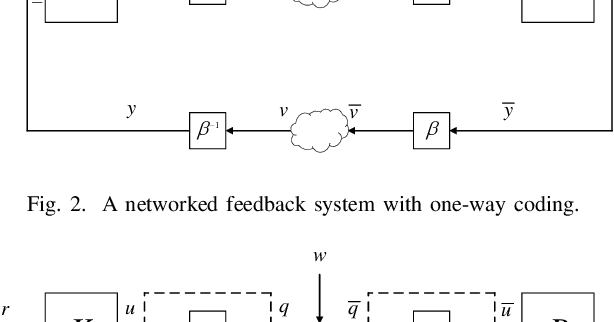
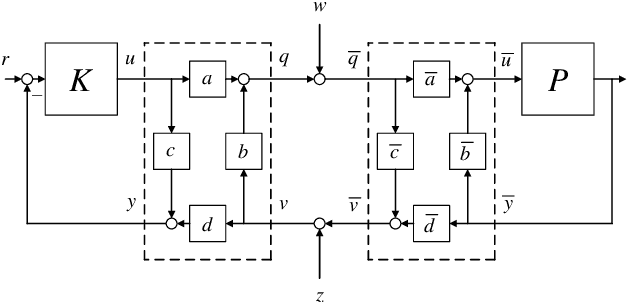
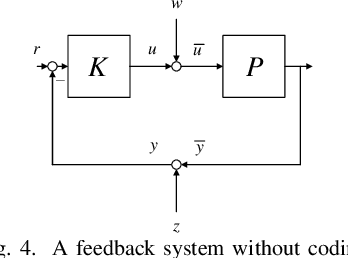
Abstract:In this paper, we introduce the concept of two-way coding, which originates in communication theory characterizing coding schemes for two-way channels, into control theory, particularly to facilitate the analysis and design of feedback control systems under injection attacks. Moreover, we propose the notion of attack decoupling, and show how the controller and the two-way coding can be co-designed to nullify the transfer function from attack to plant, rendering the attack effect zero both in transient phase and in steady state.
Generic Variance Bounds on Estimation and Prediction Errors in Time Series Analysis: An Entropy Perspective
Apr 15, 2019Abstract:In this paper, we obtain generic bounds on the variances of estimation and prediction errors in time series analysis via an information-theoretic approach. It is seen in general that the error bounds are determined by the conditional entropy of the data point to be estimated or predicted given the side information or past observations. Additionally, we discover that in order to achieve the prediction error bounds asymptotically, the necessary and sufficient condition is that the "innovation" is asymptotically white Gaussian. When restricted to Gaussian processes and 1-step prediction, our bounds are shown to reduce to the Kolmogorov-Szeg\"o formula and Wiener-Masani formula known from linear prediction theory.
A Frequency-Domain Characterization of Optimal Error Covariance for the Kalman-Bucy Filter
Jul 23, 2018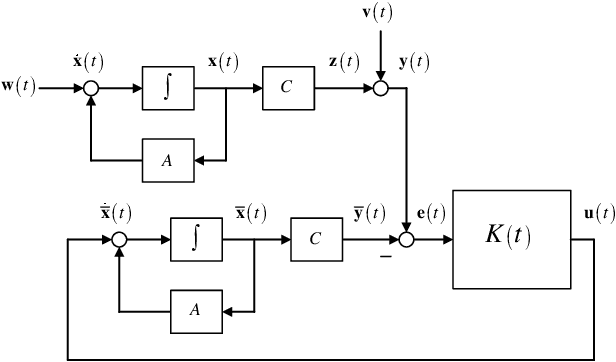
Abstract:In this paper, we discover that the trace of the division of the optimal output estimation error covariance over the noise covariance attained by the Kalman-Bucy filter can be explicitly expressed in terms of the plant dynamics and noise statistics in a frequency-domain integral characterization. Towards this end, we examine the algebraic Riccati equation associated with Kalman-Bucy filtering using analytic function theory and relate it to the Bode integral. Our approach features an alternative, frequency-domain framework for analyzing algebraic Riccati equations and reduces to various existing related results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge