HDGS: Textured 2D Gaussian Splatting for Enhanced Scene Rendering

Recent advancements in neural rendering, particularly 2D Gaussian Splatting (2DGS), have shown promising results for jointly reconstructing fine appearance and geometry by leveraging 2D Gaussian surfels. However, current methods face significant challenges when rendering at arbitrary viewpoints, such as anti-aliasing for down-sampled rendering, and texture detail preservation for high-resolution rendering. We proposed a novel method to align the 2D surfels with texture maps and augment it with per-ray depth sorting and fisher-based pruning for rendering consistency and efficiency. With correct order, per-surfel texture maps significantly improve the capabilities to capture fine details. Additionally, to render high-fidelity details in varying viewpoints, we designed a frustum-based sampling method to mitigate the aliasing artifacts. Experimental results on benchmarks and our custom texture-rich dataset demonstrate that our method surpasses existing techniques, particularly in detail preservation and anti-aliasing.

Taming False Positives in Out-of-Distribution Detection with Human Feedback

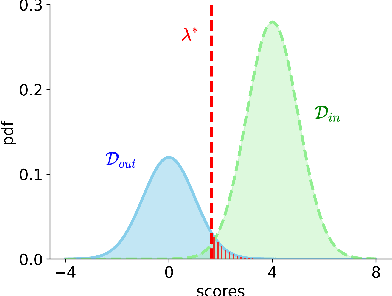
Robustness to out-of-distribution (OOD) samples is crucial for safely deploying machine learning models in the open world. Recent works have focused on designing scoring functions to quantify OOD uncertainty. Setting appropriate thresholds for these scoring functions for OOD detection is challenging as OOD samples are often unavailable up front. Typically, thresholds are set to achieve a desired true positive rate (TPR), e.g., $95\%$ TPR. However, this can lead to very high false positive rates (FPR), ranging from 60 to 96\%, as observed in the Open-OOD benchmark. In safety-critical real-life applications, e.g., medical diagnosis, controlling the FPR is essential when dealing with various OOD samples dynamically. To address these challenges, we propose a mathematically grounded OOD detection framework that leverages expert feedback to \emph{safely} update the threshold on the fly. We provide theoretical results showing that it is guaranteed to meet the FPR constraint at all times while minimizing the use of human feedback. Another key feature of our framework is that it can work with any scoring function for OOD uncertainty quantification. Empirical evaluation of our system on synthetic and benchmark OOD datasets shows that our method can maintain FPR at most $5\%$ while maximizing TPR.

Good Data from Bad Models : Foundations of Threshold-based Auto-labeling

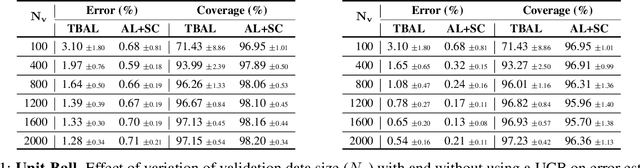
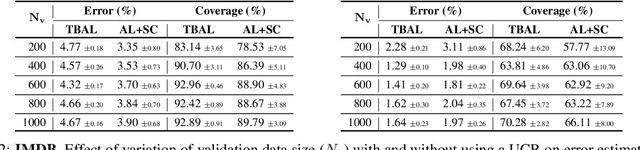
Creating large-scale high-quality labeled datasets is a major bottleneck in supervised machine learning workflows. Auto-labeling systems are a promising way to reduce reliance on manual labeling for dataset construction. Threshold-based auto-labeling, where validation data obtained from humans is used to find a threshold for confidence above which the data is machine-labeled, is emerging as a popular solution used widely in practice. Given the long shelf-life and diverse usage of the resulting datasets, understanding when the data obtained by such auto-labeling systems can be relied on is crucial. In this work, we analyze threshold-based auto-labeling systems and derive sample complexity bounds on the amount of human-labeled validation data required for guaranteeing the quality of machine-labeled data. Our results provide two insights. First, reasonable chunks of the unlabeled data can be automatically and accurately labeled by seemingly bad models. Second, a hidden downside of threshold-based auto-labeling systems is potentially prohibitive validation data usage. Together, these insights describe the promise and pitfalls of using such systems. We validate our theoretical guarantees with simulations and study the efficacy of threshold-based auto-labeling on real datasets.

Geometry of the Minimum Volume Confidence Sets

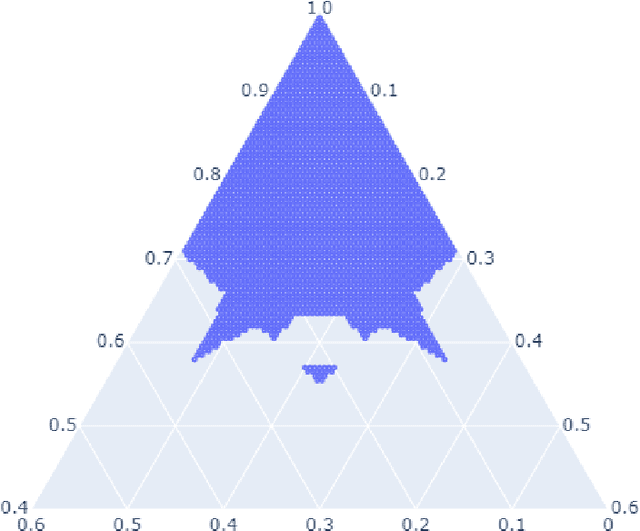
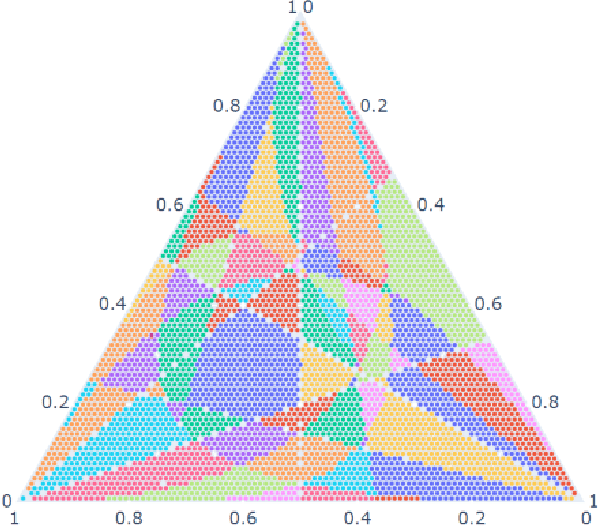
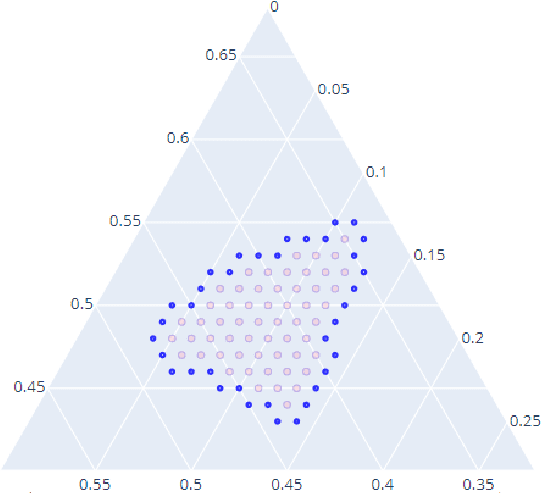
Computation of confidence sets is central to data science and machine learning, serving as the workhorse of A/B testing and underpinning the operation and analysis of reinforcement learning algorithms. This paper studies the geometry of the minimum-volume confidence sets for the multinomial parameter. When used in place of more standard confidence sets and intervals based on bounds and asymptotic approximation, learning algorithms can exhibit improved sample complexity. Prior work showed the minimum-volume confidence sets are the level-sets of a discontinuous function defined by an exact p-value. While the confidence sets are optimal in that they have minimum average volume, computation of membership of a single point in the set is challenging for problems of modest size. Since the confidence sets are level-sets of discontinuous functions, little is apparent about their geometry. This paper studies the geometry of the minimum volume confidence sets by enumerating and covering the continuous regions of the exact p-value function. This addresses a fundamental question in A/B testing: given two multinomial outcomes, how can one determine if their corresponding minimum volume confidence sets are disjoint? We answer this question in a restricted setting.