TransFusion: Contrastive Learning with Transformers

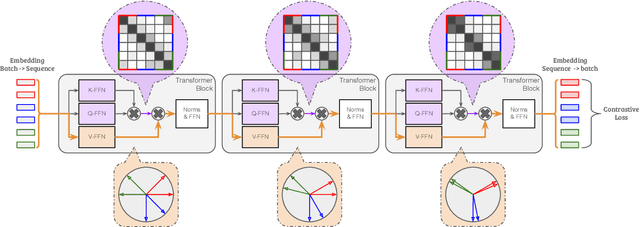
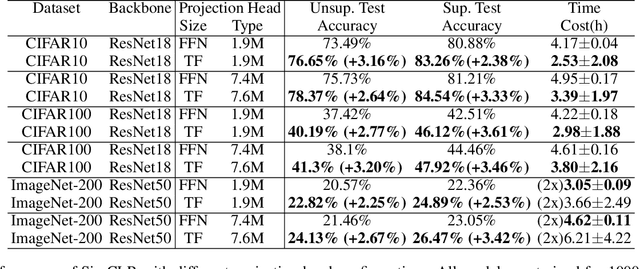
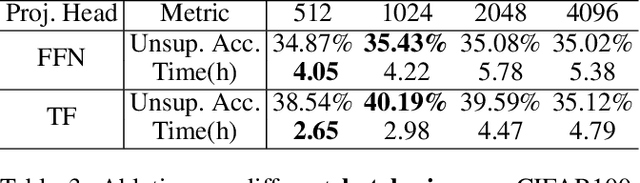
This paper proposes a novel framework, TransFusion, designed to make the process of contrastive learning more analytical and explainable. TransFusion consists of attention blocks whose softmax being replaced by ReLU, and its final block's weighted-sum operation is truncated to leave the adjacency matrix as the output. The model is trained by minimizing the Jensen-Shannon Divergence between its output and the target affinity matrix, which indicates whether each pair of samples belongs to the same or different classes. The main contribution of TransFusion lies in defining a theoretical limit for answering two fundamental questions in the field: the maximum level of data augmentation and the minimum batch size required for effective contrastive learning. Furthermore, experimental results indicate that TransFusion successfully extracts features that isolate clusters from complex real-world data, leading to improved classification accuracy in downstream tasks.

Contrastive Learning with Orthonormal Anchors (CLOA)

This study focuses on addressing the instability issues prevalent in contrastive learning, specifically examining the InfoNCE loss function and its derivatives. We reveal a critical observation that these loss functions exhibit a restrictive behavior, leading to a convergence phenomenon where embeddings tend to merge into a singular point. This "over-fusion" effect detrimentally affects classification accuracy in subsequent supervised-learning tasks. Through theoretical analysis, we demonstrate that embeddings, when equalized or confined to a rank-1 linear subspace, represent a local minimum for InfoNCE. In response to this challenge, our research introduces an innovative strategy that leverages the same or fewer labeled data than typically used in the fine-tuning phase. The loss we proposed, Orthonormal Anchor Regression Loss, is designed to disentangle embedding clusters, significantly enhancing the distinctiveness of each embedding while simultaneously ensuring their aggregation into dense, well-defined clusters. Our method demonstrates remarkable improvements with just a fraction of the conventional label requirements, as evidenced by our results on CIFAR10 and CIFAR100 datasets.

Fusion Subspace Clustering for Incomplete Data

This paper introduces {\em fusion subspace clustering}, a novel method to learn low-dimensional structures that approximate large scale yet highly incomplete data. The main idea is to assign each datum to a subspace of its own, and minimize the distance between the subspaces of all data, so that subspaces of the same cluster get {\em fused} together. Our method allows low, high, and even full-rank data; it directly accounts for noise, and its sample complexity approaches the information-theoretic limit. In addition, our approach provides a natural model selection {\em clusterpath}, and a direct completion method. We give convergence guarantees, analyze computational complexity, and show through extensive experiments on real and synthetic data that our approach performs comparably to the state-of-the-art with complete data, and dramatically better if data is missing.

Geometry of the Minimum Volume Confidence Sets

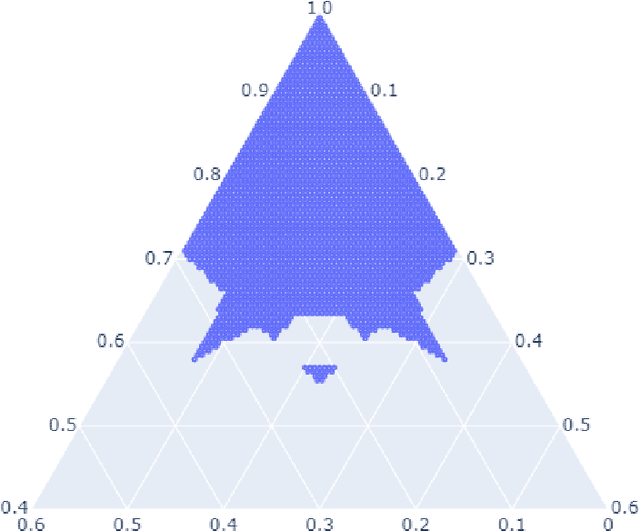
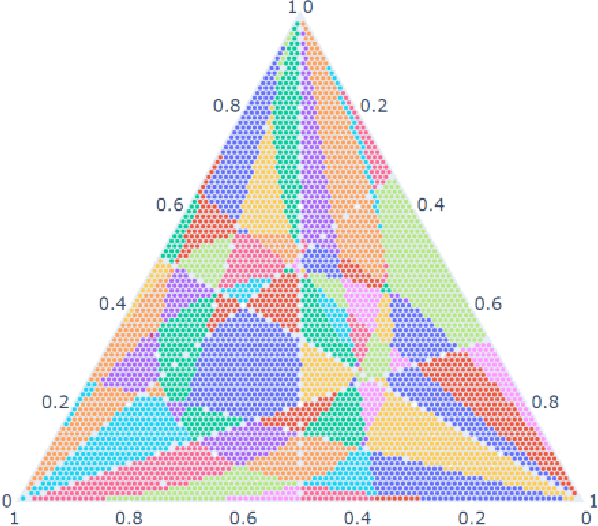
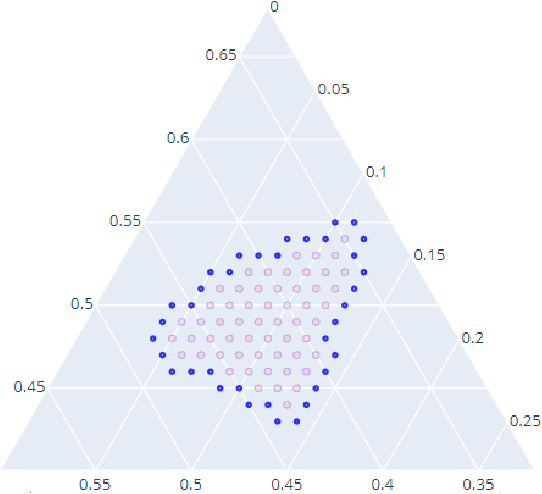
Computation of confidence sets is central to data science and machine learning, serving as the workhorse of A/B testing and underpinning the operation and analysis of reinforcement learning algorithms. This paper studies the geometry of the minimum-volume confidence sets for the multinomial parameter. When used in place of more standard confidence sets and intervals based on bounds and asymptotic approximation, learning algorithms can exhibit improved sample complexity. Prior work showed the minimum-volume confidence sets are the level-sets of a discontinuous function defined by an exact p-value. While the confidence sets are optimal in that they have minimum average volume, computation of membership of a single point in the set is challenging for problems of modest size. Since the confidence sets are level-sets of discontinuous functions, little is apparent about their geometry. This paper studies the geometry of the minimum volume confidence sets by enumerating and covering the continuous regions of the exact p-value function. This addresses a fundamental question in A/B testing: given two multinomial outcomes, how can one determine if their corresponding minimum volume confidence sets are disjoint? We answer this question in a restricted setting.

Tensor Methods for Nonlinear Matrix Completion

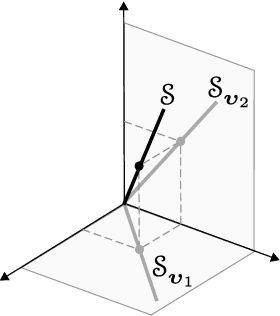
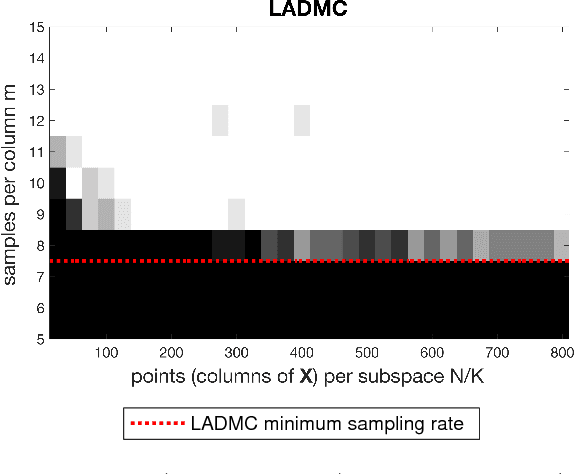
In the low rank matrix completion (LRMC) problem, the low rank assumption means that the columns (or rows) of the matrix to be completed are points on a low-dimensional linear algebraic variety. This paper extends this thinking to cases where the columns are points on a low-dimensional nonlinear algebraic variety, a problem we call Low Algebraic Dimension Matrix Completion (LADMC). Matrices whose columns belong to a union of subspaces (UoS) are an important special case. We propose a LADMC algorithm that leverages existing LRMC methods on a tensorized representation of the data. For example, a second-order tensorization representation is formed by taking the outer product of each column with itself, and we consider higher order tensorizations as well. This approach will succeed in many cases where traditional LRMC is guaranteed to fail because the data are low-rank in the tensorized representation but not in the original representation. We also provide a formal mathematical justification for the success of our method. In particular, we show bounds of the rank of these data in the tensorized representation, and we prove sampling requirements to guarantee uniqueness of the solution. Interestingly, the sampling requirements of our LADMC algorithm nearly match the information theoretic lower bounds for matrix completion under a UoS model. We also provide experimental results showing that the new approach significantly outperforms existing state-of-the-art methods for matrix completion in many situations.