AbsenceBench: Language Models Can't Tell What's Missing

Large language models (LLMs) are increasingly capable of processing long inputs and locating specific information within them, as evidenced by their performance on the Needle in a Haystack (NIAH) test. However, while models excel at recalling surprising information, they still struggle to identify clearly omitted information. We introduce AbsenceBench to assesses LLMs' capacity to detect missing information across three domains: numerical sequences, poetry, and GitHub pull requests. AbsenceBench asks models to identify which pieces of a document were deliberately removed, given access to both the original and edited contexts. Despite the apparent straightforwardness of these tasks, our experiments reveal that even state-of-the-art models like Claude-3.7-Sonnet achieve only 69.6% F1-score with a modest average context length of 5K tokens. Our analysis suggests this poor performance stems from a fundamental limitation: Transformer attention mechanisms cannot easily attend to "gaps" in documents since these absences don't correspond to any specific keys that can be attended to. Overall, our results and analysis provide a case study of the close proximity of tasks where models are already superhuman (NIAH) and tasks where models breakdown unexpectedly (AbsenceBench).

How Predictable Are Large Language Model Capabilities? A Case Study on BIG-bench

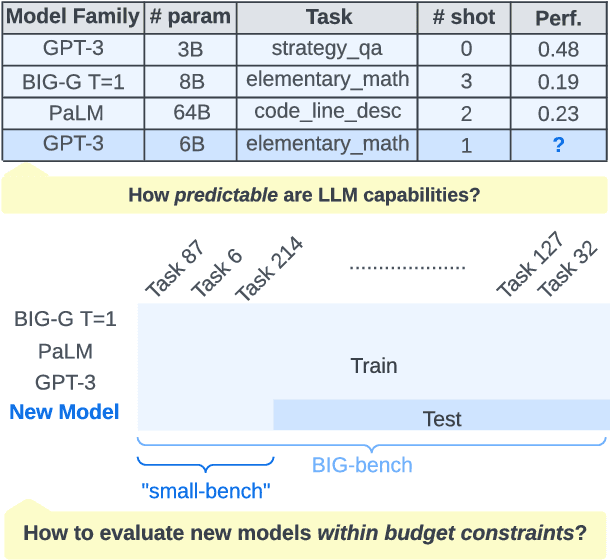
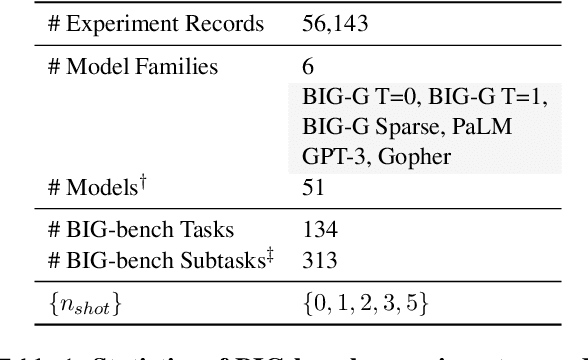
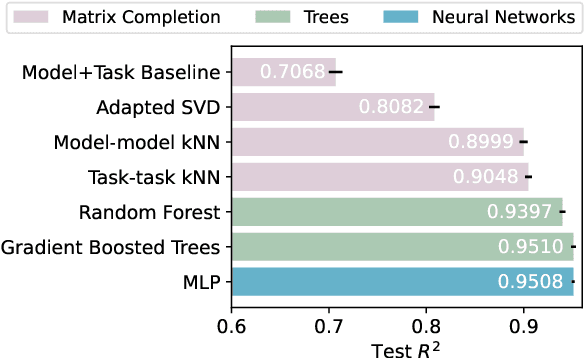
We investigate the predictability of large language model (LLM) capabilities: given records of past experiments using different model families, numbers of parameters, tasks, and numbers of in-context examples, can we accurately predict LLM performance on new experiment configurations? Answering this question has practical implications for LLM users (e.g., deciding which models to try), developers (e.g., prioritizing evaluation on representative tasks), and the research community (e.g., identifying hard-to-predict capabilities that warrant further investigation). We study the performance prediction problem on experiment records from BIG-bench. On a random train-test split, an MLP-based predictor achieves RMSE below 5%, demonstrating the presence of learnable patterns within the experiment records. Further, we formulate the problem of searching for "small-bench," an informative subset of BIG-bench tasks from which the performance of the full set can be maximally recovered, and find a subset as informative for evaluating new model families as BIG-bench Hard, while being 3x smaller.

Estimating Large Language Model Capabilities without Labeled Test Data

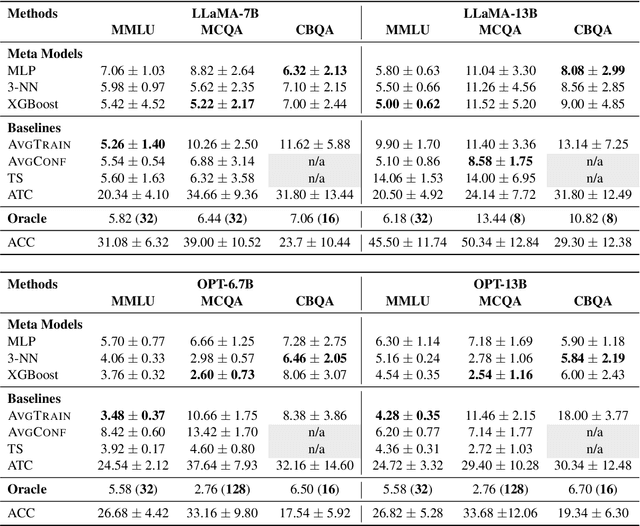
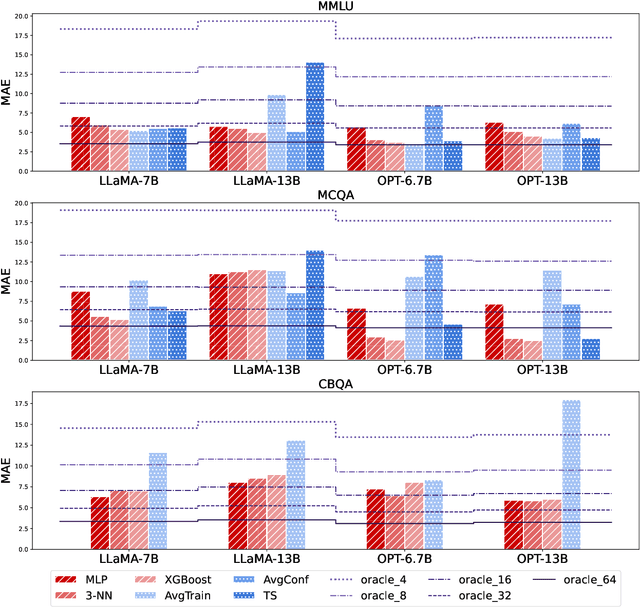
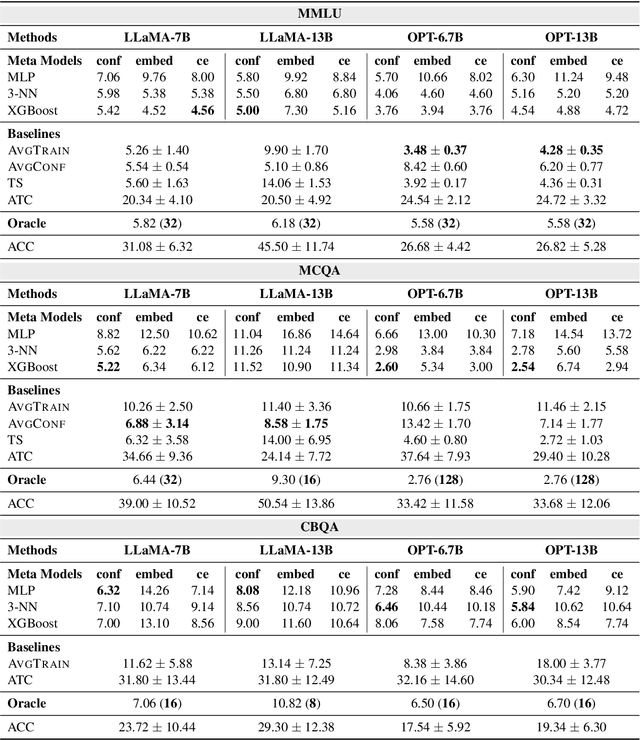
Large Language Models (LLMs) have exhibited an impressive ability to perform in-context learning (ICL) from only a few examples, but the success of ICL varies widely from task to task. Thus, it is important to quickly determine whether ICL is applicable to a new task, but directly evaluating ICL accuracy can be expensive in situations where test data is expensive to annotate -- the exact situations where ICL is most appealing. In this paper, we propose the task of ICL accuracy estimation, in which we predict the accuracy of an LLM when doing in-context learning on a new task given only unlabeled data for that task. To perform ICL accuracy estimation, we propose a method that trains a meta-model using LLM confidence scores as features. We compare our method to several strong accuracy estimation baselines on a new benchmark that covers 4 LLMs and 3 task collections. On average, the meta-model improves over all baselines and achieves the same estimation performance as directly evaluating on 40 labeled test examples per task, across the total 12 settings. We encourage future work to improve on our methods and evaluate on our ICL accuracy estimation benchmark to deepen our understanding of when ICL works.