MIK: Modified Isolation Kernel for Biological Sequence Visualization, Classification, and Clustering

The t-Distributed Stochastic Neighbor Embedding (t-SNE) has emerged as a popular dimensionality reduction technique for visualizing high-dimensional data. It computes pairwise similarities between data points by default using an RBF kernel and random initialization (in low-dimensional space), which successfully captures the overall structure but may struggle to preserve the local structure efficiently. This research proposes a novel approach called the Modified Isolation Kernel (MIK) as an alternative to the Gaussian kernel, which is built upon the concept of the Isolation Kernel. MIK uses adaptive density estimation to capture local structures more accurately and integrates robustness measures. It also assigns higher similarity values to nearby points and lower values to distant points. Comparative research using the normal Gaussian kernel, the isolation kernel, and several initialization techniques, including random, PCA, and random walk initializations, are used to assess the proposed approach (MIK). Additionally, we compare the computational efficiency of all $3$ kernels with $3$ different initialization methods. Our experimental results demonstrate several advantages of the proposed kernel (MIK) and initialization method selection. It exhibits improved preservation of the local and global structure and enables better visualization of clusters and subclusters in the embedded space. These findings contribute to advancing dimensionality reduction techniques and provide researchers and practitioners with an effective tool for data exploration, visualization, and analysis in various domains.

Position Specific Scoring Is All You Need? Revisiting Protein Sequence Classification Tasks

Understanding the structural and functional characteristics of proteins are crucial for developing preventative and curative strategies that impact fields from drug discovery to policy development. An important and popular technique for examining how amino acids make up these characteristics of the protein sequences with position-specific scoring (PSS). While the string kernel is crucial in natural language processing (NLP), it is unclear if string kernels can extract biologically meaningful information from protein sequences, despite the fact that they have been shown to be effective in the general sequence analysis tasks. In this work, we propose a weighted PSS kernel matrix (or W-PSSKM), that combines a PSS representation of protein sequences, which encodes the frequency information of each amino acid in a sequence, with the notion of the string kernel. This results in a novel kernel function that outperforms many other approaches for protein sequence classification. We perform extensive experimentation to evaluate the proposed method. Our findings demonstrate that the W-PSSKM significantly outperforms existing baselines and state-of-the-art methods and achieves up to 45.1\% improvement in classification accuracy.

Impact Of Missing Data Imputation On The Fairness And Accuracy Of Graph Node Classifiers

Analysis of the fairness of machine learning (ML) algorithms recently attracted many researchers' interest. Most ML methods show bias toward protected groups, which limits the applicability of ML models in many applications like crime rate prediction etc. Since the data may have missing values which, if not appropriately handled, are known to further harmfully affect fairness. Many imputation methods are proposed to deal with missing data. However, the effect of missing data imputation on fairness is not studied well. In this paper, we analyze the effect on fairness in the context of graph data (node attributes) imputation using different embedding and neural network methods. Extensive experiments on six datasets demonstrate severe fairness issues in missing data imputation under graph node classification. We also find that the choice of the imputation method affects both fairness and accuracy. Our results provide valuable insights into graph data fairness and how to handle missingness in graphs efficiently. This work also provides directions regarding theoretical studies on fairness in graph data.

Fair Allocation Based Soft Load Shedding

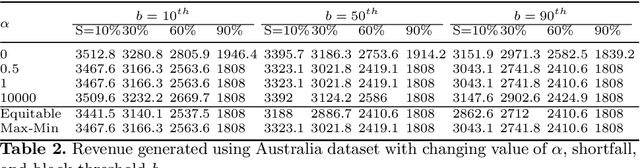
Renewable sources are taking center stage in electricity generation. Due to the intermittent nature of these renewable resources, the problem of the demand-supply gap arises. To solve this problem, several techniques have been proposed in the literature in terms of cost (adding peaker plants), availability of data (Demand Side Management "DSM"), hardware infrastructure (appliance controlling DSM) and safety (voltage reduction). However, these solutions are not fair in terms of electricity distribution. In many cases, although the available supply may not match the demand in peak hours, however, the total aggregated demand remains less than the total supply for the whole day. Load shedding (complete blackout) is a commonly used solution to deal with the demand-supply gap, which can cause substantial economic losses. To solve the demand-supply gap problem, we propose a solution called Soft Load Shedding (SLS), which assigns electricity quota to each household in a fair way. We measure the fairness of SLS by defining a function for household satisfaction level. We model the household utilities by parametric function and formulate the problem of SLS as a social welfare problem. We also consider revenue generated from the fair allocation as a performance measure. To evaluate our approach, extensive experiments have been performed on both synthetic and real-world datasets, and our model is compared with several baselines to show its effectiveness in terms of fair allocation and revenue generation.

Hour-Ahead Load Forecasting Using AMI Data

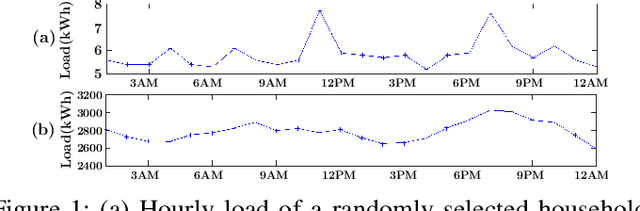
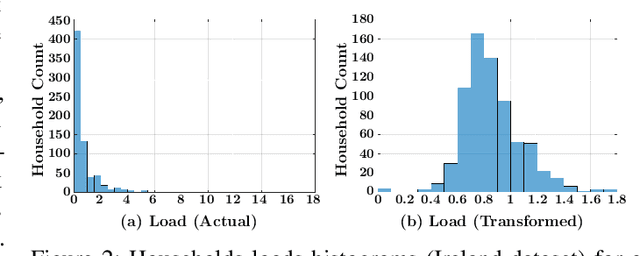
Accurate short-term load forecasting is essential for efficient operation of the power sector. Predicting load at a fine granularity such as individual households or buildings is challenging due to higher volatility and uncertainty in the load. In aggregate loads such as at grids level, the inherent stochasticity and fluctuations are averaged-out, the problem becomes substantially easier. We propose an approach for short-term load forecasting at individual consumers (households) level, called Forecasting using Matrix Factorization (FMF). FMF does not use any consumers' demographic or activity patterns information. Therefore, it can be applied to any locality with the readily available smart meters and weather data. We perform extensive experiments on three benchmark datasets and demonstrate that FMF significantly outperforms the computationally expensive state-of-the-art methods for this problem. We achieve up to 26.5% and 24.4 % improvement in RMSE over Regression Tree and Support Vector Machine, respectively and up to 36% and 73.2% improvement in MAPE over Random Forest and Long Short-Term Memory neural network, respectively.