On Surjectivity of Neural Networks: Can you elicit any behavior from your model?

Given a trained neural network, can any specified output be generated by some input? Equivalently, does the network correspond to a function that is surjective? In generative models, surjectivity implies that any output, including harmful or undesirable content, can in principle be generated by the networks, raising concerns about model safety and jailbreak vulnerabilities. In this paper, we prove that many fundamental building blocks of modern neural architectures, such as networks with pre-layer normalization and linear-attention modules, are almost always surjective. As corollaries, widely used generative frameworks, including GPT-style transformers and diffusion models with deterministic ODE solvers, admit inverse mappings for arbitrary outputs. By studying surjectivity of these modern and commonly used neural architectures, we contribute a formalism that sheds light on their unavoidable vulnerability to a broad class of adversarial attacks.

A Black-box Approach for Non-stationary Multi-agent Reinforcement Learning

We investigate learning the equilibria in non-stationary multi-agent systems and address the challenges that differentiate multi-agent learning from single-agent learning. Specifically, we focus on games with bandit feedback, where testing an equilibrium can result in substantial regret even when the gap to be tested is small, and the existence of multiple optimal solutions (equilibria) in stationary games poses extra challenges. To overcome these obstacles, we propose a versatile black-box approach applicable to a broad spectrum of problems, such as general-sum games, potential games, and Markov games, when equipped with appropriate learning and testing oracles for stationary environments. Our algorithms can achieve $\widetilde{O}\left(\Delta^{1/4}T^{3/4}\right)$ regret when the degree of nonstationarity, as measured by total variation $\Delta$, is known, and $\widetilde{O}\left(\Delta^{1/5}T^{4/5}\right)$ regret when $\Delta$ is unknown, where $T$ is the number of rounds. Meanwhile, our algorithm inherits the favorable dependence on number of agents from the oracles. As a side contribution that may be independent of interest, we show how to test for various types of equilibria by a black-box reduction to single-agent learning, which includes Nash equilibria, correlated equilibria, and coarse correlated equilibria.

Offline Meta Reinforcement Learning with In-Distribution Online Adaptation

Recent offline meta-reinforcement learning (meta-RL) methods typically utilize task-dependent behavior policies (e.g., training RL agents on each individual task) to collect a multi-task dataset. However, these methods always require extra information for fast adaptation, such as offline context for testing tasks. To address this problem, we first formally characterize a unique challenge in offline meta-RL: transition-reward distribution shift between offline datasets and online adaptation. Our theory finds that out-of-distribution adaptation episodes may lead to unreliable policy evaluation and that online adaptation with in-distribution episodes can ensure adaptation performance guarantee. Based on these theoretical insights, we propose a novel adaptation framework, called In-Distribution online Adaptation with uncertainty Quantification (IDAQ), which generates in-distribution context using a given uncertainty quantification and performs effective task belief inference to address new tasks. We find a return-based uncertainty quantification for IDAQ that performs effectively. Experiments show that IDAQ achieves state-of-the-art performance on the Meta-World ML1 benchmark compared to baselines with/without offline adaptation.

Practically Solving LPN in High Noise Regimes Faster Using Neural Networks

We conduct a systematic study of solving the learning parity with noise problem (LPN) using neural networks. Our main contribution is designing families of two-layer neural networks that practically outperform classical algorithms in high-noise, low-dimension regimes. We consider three settings where the numbers of LPN samples are abundant, very limited, and in between. In each setting we provide neural network models that solve LPN as fast as possible. For some settings we are also able to provide theories that explain the rationale of the design of our models. Comparing with the previous experiments of Esser, Kubler, and May (CRYPTO 2017), for dimension $n = 26$, noise rate $\tau = 0.498$, the ''Guess-then-Gaussian-elimination'' algorithm takes 3.12 days on 64 CPU cores, whereas our neural network algorithm takes 66 minutes on 8 GPUs. Our algorithm can also be plugged into the hybrid algorithms for solving middle or large dimension LPN instances.

Offline congestion games: How feedback type affects data coverage requirement

This paper investigates when one can efficiently recover an approximate Nash Equilibrium (NE) in offline congestion games.The existing dataset coverage assumption in offline general-sum games inevitably incurs a dependency on the number of actions, which can be exponentially large in congestion games. We consider three different types of feedback with decreasing revealed information. Starting from the facility-level (a.k.a., semi-bandit) feedback, we propose a novel one-unit deviation coverage condition and give a pessimism-type algorithm that can recover an approximate NE. For the agent-level (a.k.a., bandit) feedback setting, interestingly, we show the one-unit deviation coverage condition is not sufficient. On the other hand, we convert the game to multi-agent linear bandits and show that with a generalized data coverage assumption in offline linear bandits, we can efficiently recover the approximate NE. Lastly, we consider a novel type of feedback, the game-level feedback where only the total reward from all agents is revealed. Again, we show the coverage assumption for the agent-level feedback setting is insufficient in the game-level feedback setting, and with a stronger version of the data coverage assumption for linear bandits, we can recover an approximate NE. Together, our results constitute the first study of offline congestion games and imply formal separations between different types of feedback.

Offline Reinforcement Learning with Reverse Model-based Imagination

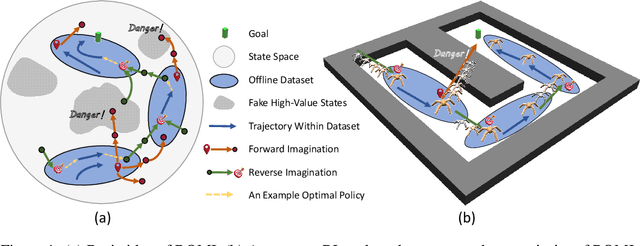
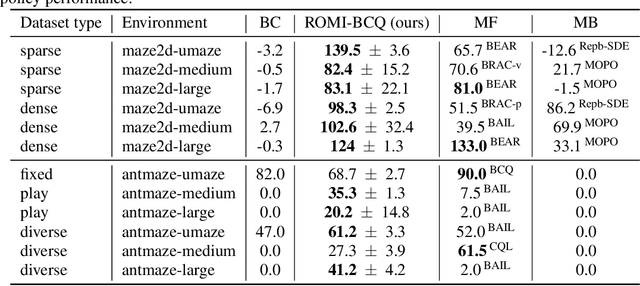
In offline reinforcement learning (offline RL), one of the main challenges is to deal with the distributional shift between the learning policy and the given dataset. To address this problem, recent offline RL methods attempt to introduce conservatism bias to encourage learning on high-confidence areas. Model-free approaches directly encode such bias into policy or value function learning using conservative regularizations or special network structures, but their constrained policy search limits the generalization beyond the offline dataset. Model-based approaches learn forward dynamics models with conservatism quantifications and then generate imaginary trajectories to extend the offline datasets. However, due to limited samples in offline dataset, conservatism quantifications often suffer from overgeneralization in out-of-support regions. The unreliable conservative measures will mislead forward model-based imaginations to undesired areas, leading to overaggressive behaviors. To encourage more conservatism, we propose a novel model-based offline RL framework, called Reverse Offline Model-based Imagination (ROMI). We learn a reverse dynamics model in conjunction with a novel reverse policy, which can generate rollouts leading to the target goal states within the offline dataset. These reverse imaginations provide informed data augmentation for the model-free policy learning and enable conservative generalization beyond the offline dataset. ROMI can effectively combine with off-the-shelf model-free algorithms to enable model-based generalization with proper conservatism. Empirical results show that our method can generate more conservative behaviors and achieve state-of-the-art performance on offline RL benchmark tasks.