Age Optimal Sampling for Unreliable Channels under Unknown Channel Statistics

In this paper, we study a system in which a sensor forwards status updates to a receiver through an error-prone channel, while the receiver sends the transmission results back to the sensor via a reliable channel. Both channels are subject to random delays. To evaluate the timeliness of the status information at the receiver, we use the Age of Information (AoI) metric. The objective is to design a sampling policy that minimizes the expected time-average AoI, even when the channel statistics (e.g., delay distributions) are unknown. We first review the threshold structure of the optimal offline policy under known channel statistics and then reformulate the design of the online algorithm as a stochastic approximation problem. We propose a Robbins-Monro algorithm to solve this problem and demonstrate that the optimal threshold can be approximated almost surely. Moreover, we prove that the cumulative AoI regret of the online algorithm increases with rate $\mathcal{O}(\ln K)$, where $K$ is the number of successful transmissions. In addition, our algorithm is shown to be minimax order optimal, in the sense that for any online learning algorithm, the cumulative AoI regret up to the $K$-th successful transmissions grows with the rate at least $\Omega(\ln K)$ in the worst case delay distribution. Finally, we improve the stability of the proposed online learning algorithm through a momentum-based stochastic gradient descent algorithm. Simulation results validate the performance of our proposed algorithm.

Solving General Noisy Inverse Problem via Posterior Sampling: A Policy Gradient Viewpoint

Solving image inverse problems (e.g., super-resolution and inpainting) requires generating a high fidelity image that matches the given input (the low-resolution image or the masked image). By using the input image as guidance, we can leverage a pretrained diffusion generative model to solve a wide range of image inverse tasks without task specific model fine-tuning. To precisely estimate the guidance score function of the input image, we propose Diffusion Policy Gradient (DPG), a tractable computation method by viewing the intermediate noisy images as policies and the target image as the states selected by the policy. Experiments show that our method is robust to both Gaussian and Poisson noise degradation on multiple linear and non-linear inverse tasks, resulting into a higher image restoration quality on FFHQ, ImageNet and LSUN datasets.

Age Optimum Sampling in Non-Stationary Environment

In this work, we consider a status update system with a sensor and a receiver. The status update information is sampled by the sensor and then forwarded to the receiver through a channel with non-stationary delay distribution. The data freshness at the receiver is quantified by the Age-of-Information (AoI). The goal is to design an online sampling strategy that can minimize the average AoI when the non-stationary delay distribution is unknown. Assuming that channel delay distribution may change over time, to minimize the average AoI, we propose a joint stochastic approximation and non-parametric change point detection algorithm that can: (1) learn the optimum update threshold when the delay distribution remains static; (2) detect the change in transmission delay distribution quickly and then restart the learning process. Simulation results show that the proposed algorithm can quickly detect the delay changes, and the average AoI obtained by the proposed policy converges to the minimum AoI.

On the Generative Utility of Cyclic Conditionals

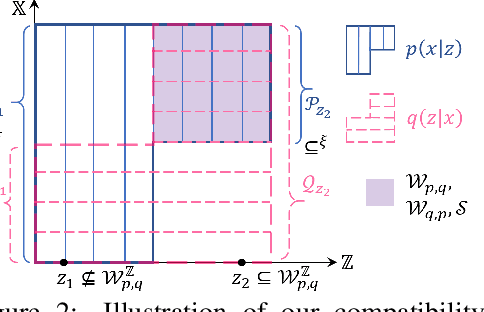
We study whether and how can we model a joint distribution $p(x,z)$ using two conditional models $p(x|z)$ and $q(z|x)$ that form a cycle. This is motivated by the observation that deep generative models, in addition to a likelihood model $p(x|z)$, often also use an inference model $q(z|x)$ for data representation, but they rely on a usually uninformative prior distribution $p(z)$ to define a joint distribution, which may render problems like posterior collapse and manifold mismatch. To explore the possibility to model a joint distribution using only $p(x|z)$ and $q(z|x)$, we study their compatibility and determinacy, corresponding to the existence and uniqueness of a joint distribution whose conditional distributions coincide with them. We develop a general theory for novel and operable equivalence criteria for compatibility, and sufficient conditions for determinacy. Based on the theory, we propose the CyGen framework for cyclic-conditional generative modeling, including methods to enforce compatibility and use the determined distribution to fit and generate data. With the prior constraint removed, CyGen better fits data and captures more representative features, supported by experiments showing better generation and downstream classification performance.