WalnutData: A UAV Remote Sensing Dataset of Green Walnuts and Model Evaluation

The UAV technology is gradually maturing and can provide extremely powerful support for smart agriculture and precise monitoring. Currently, there is no dataset related to green walnuts in the field of agricultural computer vision. Thus, in order to promote the algorithm design in the field of agricultural computer vision, we used UAV to collect remote-sensing data from 8 walnut sample plots. Considering that green walnuts are subject to various lighting conditions and occlusion, we constructed a large-scale dataset with a higher-granularity of target features - WalnutData. This dataset contains a total of 30,240 images and 706,208 instances, and there are 4 target categories: being illuminated by frontal light and unoccluded (A1), being backlit and unoccluded (A2), being illuminated by frontal light and occluded (B1), and being backlit and occluded (B2). Subsequently, we evaluated many mainstream algorithms on WalnutData and used these evaluation results as the baseline standard. The dataset and all evaluation results can be obtained at https://github.com/1wuming/WalnutData.

Shedding Light on the Polymer's Identity: Microplastic Detection and Identification Through Nile Red Staining and Multispectral Imaging (FIMAP)

The widespread distribution of microplastics (MPs) in the environment presents significant challenges for their detection and identification. Fluorescence imaging has emerged as a promising technique for enhancing plastic particle detectability and enabling accurate classification based on fluorescence behavior. However, conventional segmentation techniques face limitations, including poor signal-to-noise ratio, inconsistent illumination, thresholding difficulties, and false positives from natural organic matter (NOM). To address these challenges, this study introduces the Fluorescence Imaging Microplastic Analysis Platform (FIMAP), a retrofitted multispectral camera with four optical filters and five excitation wavelengths. FIMAP enables comprehensive characterization of the fluorescence behavior of ten Nile Red-stained MPs: HDPE, LDPE, PP, PS, EPS, ABS, PVC, PC, PET, and PA, while effectively excluding NOM. Using K-means clustering for robust segmentation (Intersection over Union = 0.877) and a 20-dimensional color coordinate multivariate nearest neighbor approach for MP classification (>3.14 mm), FIMAP achieves 90% precision, 90% accuracy, 100% recall, and an F1 score of 94.7%. Only PS was occasionally misclassified as EPS. For smaller MPs (35-104 microns), classification accuracy declined, likely due to reduced stain sorption, fewer detectable pixels, and camera instability. Integrating FIMAP with higher-magnification instruments, such as a microscope, may enhance MP identification. This study presents FIMAP as an automated, high-throughput framework for detecting and classifying MPs across large environmental sample volumes.

Physics-Constrained Neural Network for the Analysis and Feature-Based Optimization of Woven Composites

Woven composites are produced by interlacing warp and weft fibers in a pattern or weave style. By changing the pattern or material, the mechanical properties of woven composites can be significantly changed; however, the role of woven composite architecture (pattern, material) on the mechanical properties is not well understood. In this paper, we explore the relationship between woven composite architectures (weave pattern, weave material sequence) and the corresponding modulus through our proposed Physics-Constrained Neural Network (PCNN). Furthermore, we apply statistical learning methods to optimize the woven composite architecture to improve mechanical responses. Our results show that PCNN can effectively predict woven architecture for the desired modulus with much higher accuracy than several baseline models. PCNN can be further combined with feature-based optimization to determine the optimal woven composite architecture at the initial design stage. In addition to relating woven composite architecture to its mechanical responses, our research also provides an in-depth understanding of how architectural features govern mechanical responses. We anticipate our proposed frameworks will primarily facilitate the woven composite analysis and optimization process and be a starting point to introduce Physics knowledge-guided Neural Networks into the complex structural analysis.

Difference-Based Deep Learning Framework for Stress Predictions in Heterogeneous Media

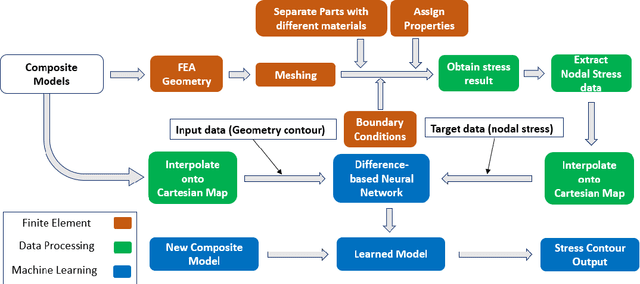
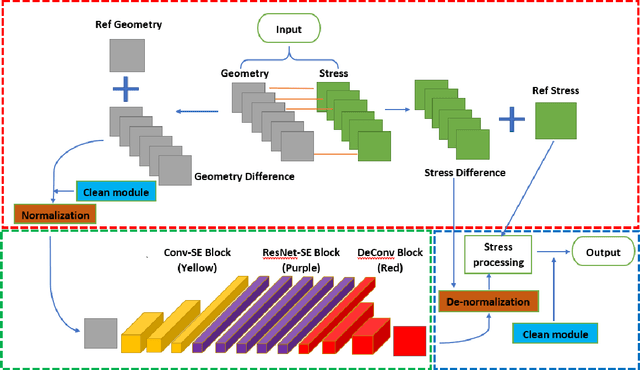
Stress analysis of heterogeneous media, like composite materials, using finite element method (FEM) has become commonplace in design and analysis. However, calculating stresses and determining stress distributions in heterogeneous media using FEM can be computationally expensive in situations like optimization and multi-scaling, where several design iterations are required to be tested iteratively until convergence. In this paper, we utilize deep learning and develop a set of Difference-based Neural Network (DNN) frameworks based on engineering and statistics knowledge to determine stress distribution in heterogeneous media with special focus on discontinuous domains that manifest high stress concentrations. To evaluate the performance of DNN frameworks, we consider four different types of geometric models that are commonly used in the analysis of composite materials: plate with circular cutout, square packed fiber reinforced, hexagonal packed fiber reinforced and hollow particle reinforced models. The proposed DNN structure consists of a normalization module (DNN-N) for all geometries considered, while we additionally introduce a clean module with DNN-N, named DNN-NC, for geometries with discontinuities. Results show that the DNN structures (DNN-N and DNN-NC) significantly enhance the accuracy of stress prediction compared to existing structures for all four models considered, especially when localized high stress concentrations are present in the geometric models.