Difference-Based Deep Learning Framework for Stress Predictions in Heterogeneous Media

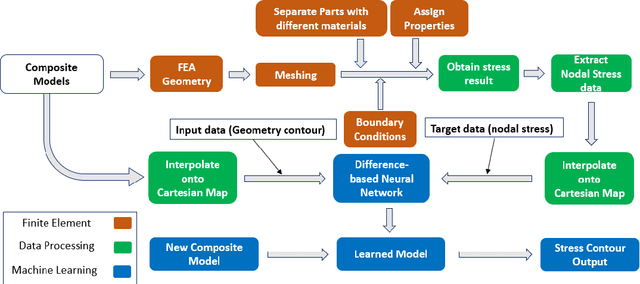
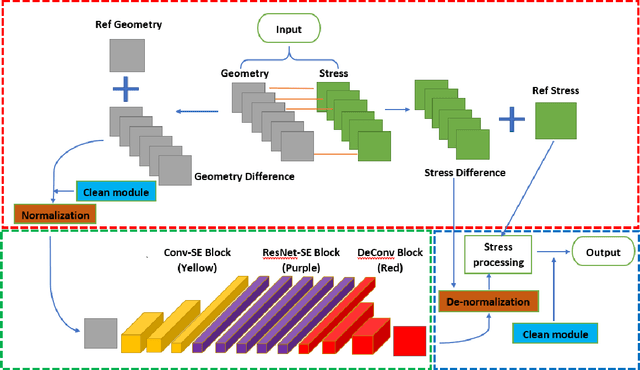
Stress analysis of heterogeneous media, like composite materials, using finite element method (FEM) has become commonplace in design and analysis. However, calculating stresses and determining stress distributions in heterogeneous media using FEM can be computationally expensive in situations like optimization and multi-scaling, where several design iterations are required to be tested iteratively until convergence. In this paper, we utilize deep learning and develop a set of Difference-based Neural Network (DNN) frameworks based on engineering and statistics knowledge to determine stress distribution in heterogeneous media with special focus on discontinuous domains that manifest high stress concentrations. To evaluate the performance of DNN frameworks, we consider four different types of geometric models that are commonly used in the analysis of composite materials: plate with circular cutout, square packed fiber reinforced, hexagonal packed fiber reinforced and hollow particle reinforced models. The proposed DNN structure consists of a normalization module (DNN-N) for all geometries considered, while we additionally introduce a clean module with DNN-N, named DNN-NC, for geometries with discontinuities. Results show that the DNN structures (DNN-N and DNN-NC) significantly enhance the accuracy of stress prediction compared to existing structures for all four models considered, especially when localized high stress concentrations are present in the geometric models.