Reparameterizing the Birkhoff Polytope for Variational Permutation Inference

Many matching, tracking, sorting, and ranking problems require probabilistic reasoning about possible permutations, a set that grows factorially with dimension. Combinatorial optimization algorithms may enable efficient point estimation, but fully Bayesian inference poses a severe challenge in this high-dimensional, discrete space. To surmount this challenge, we start with the usual step of relaxing a discrete set (here, of permutation matrices) to its convex hull, which here is the Birkhoff polytope: the set of all doubly-stochastic matrices. We then introduce two novel transformations: first, an invertible and differentiable stick-breaking procedure that maps unconstrained space to the Birkhoff polytope; second, a map that rounds points toward the vertices of the polytope. Both transformations include a temperature parameter that, in the limit, concentrates the densities on permutation matrices. We then exploit these transformations and reparameterization gradients to introduce variational inference over permutation matrices, and we demonstrate its utility in a series of experiments.

Learning Graph Topological Features via GAN

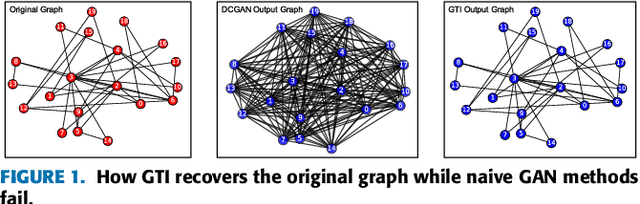
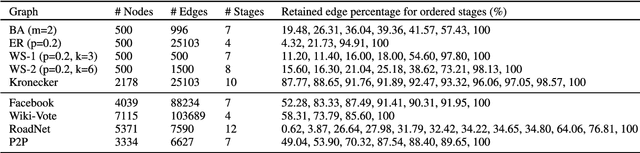
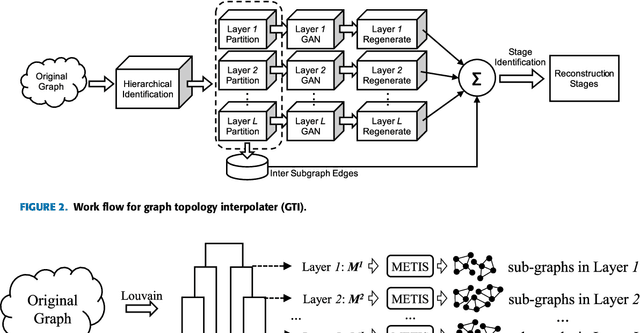
Inspired by the generation power of generative adversarial networks (GANs) in image domains, we introduce a novel hierarchical architecture for learning characteristic topological features from a single arbitrary input graph via GANs. The hierarchical architecture consisting of multiple GANs preserves both local and global topological features and automatically partitions the input graph into representative stages for feature learning. The stages facilitate reconstruction and can be used as indicators of the importance of the associated topological structures. Experiments show that our method produces subgraphs retaining a wide range of topological features, even in early reconstruction stages (unlike a single GAN, which cannot easily identify such features, let alone reconstruct the original graph). This paper is firstline research on combining the use of GANs and graph topological analysis.

Can GAN Learn Topological Features of a Graph?

This paper is first-line research expanding GANs into graph topology analysis. By leveraging the hierarchical connectivity structure of a graph, we have demonstrated that generative adversarial networks (GANs) can successfully capture topological features of any arbitrary graph, and rank edge sets by different stages according to their contribution to topology reconstruction. Moreover, in addition to acting as an indicator of graph reconstruction, we find that these stages can also preserve important topological features in a graph.