A Thermal Machine Learning Solver For Chip Simulation

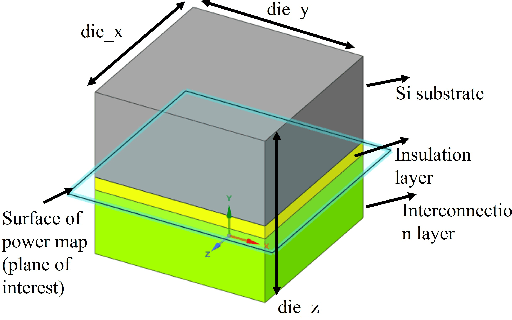
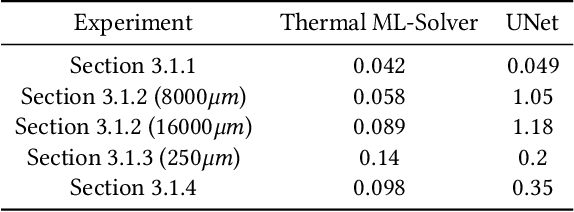
Thermal analysis provides deeper insights into electronic chips behavior under different temperature scenarios and enables faster design exploration. However, obtaining detailed and accurate thermal profile on chip is very time-consuming using FEM or CFD. Therefore, there is an urgent need for speeding up the on-chip thermal solution to address various system scenarios. In this paper, we propose a thermal machine-learning (ML) solver to speed-up thermal simulations of chips. The thermal ML-Solver is an extension of the recent novel approach, CoAEMLSim (Composable Autoencoder Machine Learning Simulator) with modifications to the solution algorithm to handle constant and distributed HTC. The proposed method is validated against commercial solvers, such as Ansys MAPDL, as well as a latest ML baseline, UNet, under different scenarios to demonstrate its enhanced accuracy, scalability, and generalizability.

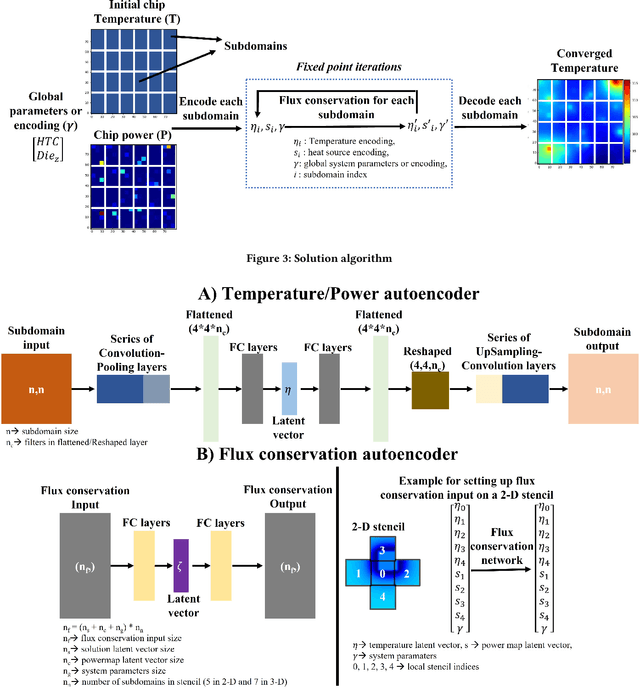
A composable autoencoder-based iterative algorithm for accelerating numerical simulations

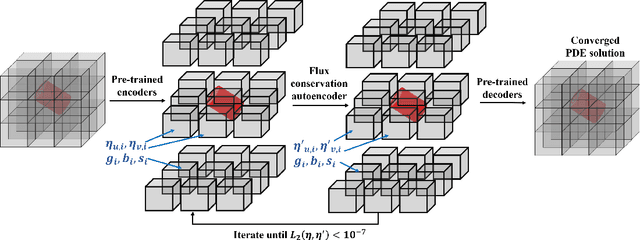
Numerical simulations for engineering applications solve partial differential equations (PDE) to model various physical processes. Traditional PDE solvers are very accurate but computationally costly. On the other hand, Machine Learning (ML) methods offer a significant computational speedup but face challenges with accuracy and generalization to different PDE conditions, such as geometry, boundary conditions, initial conditions and PDE source terms. In this work, we propose a novel ML-based approach, CoAE-MLSim (Composable AutoEncoder Machine Learning Simulation), which is an unsupervised, lower-dimensional, local method, that is motivated from key ideas used in commercial PDE solvers. This allows our approach to learn better with relatively fewer samples of PDE solutions. The proposed ML-approach is compared against commercial solvers for better benchmarks as well as latest ML-approaches for solving PDEs. It is tested for a variety of complex engineering cases to demonstrate its computational speed, accuracy, scalability, and generalization across different PDE conditions. The results show that our approach captures physics accurately across all metrics of comparison (including measures such as results on section cuts and lines).

Geometry encoding for numerical simulations

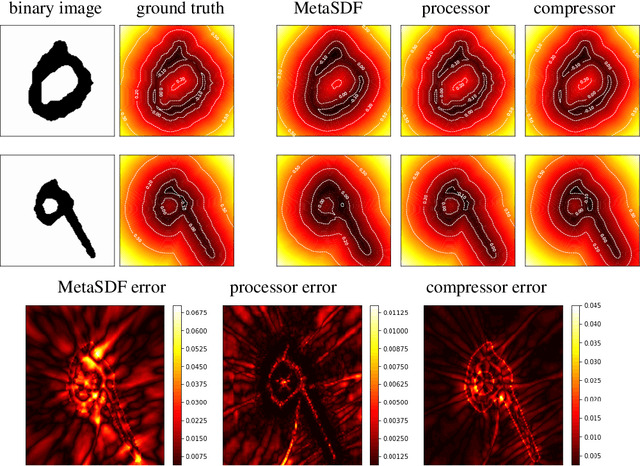
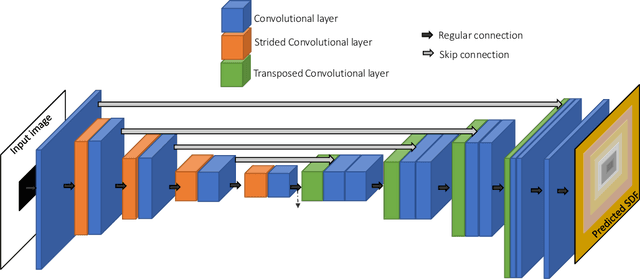
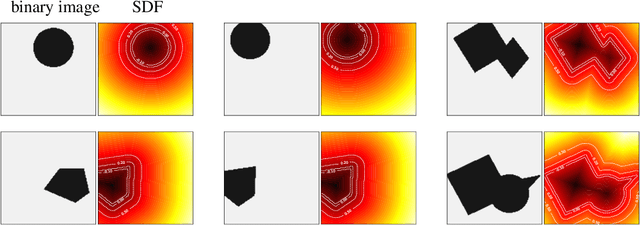
We present a notion of geometry encoding suitable for machine learning-based numerical simulation. In particular, we delineate how this notion of encoding is different than other encoding algorithms commonly used in other disciplines such as computer vision and computer graphics. We also present a model comprised of multiple neural networks including a processor, a compressor and an evaluator.These parts each satisfy a particular requirement of our encoding. We compare our encoding model with the analogous models in the literature

One-shot learning for solution operators of partial differential equations

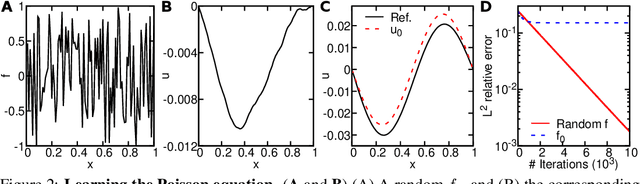
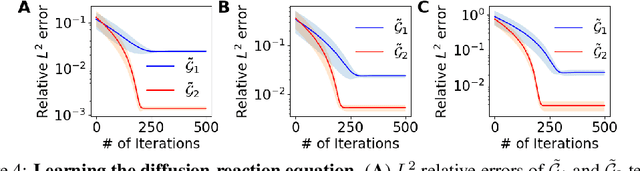
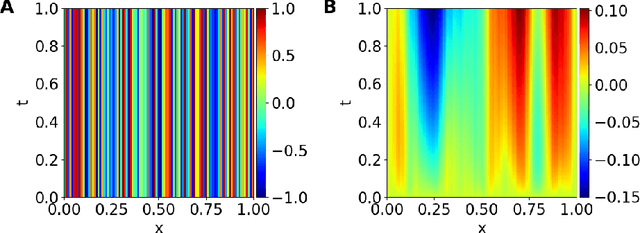
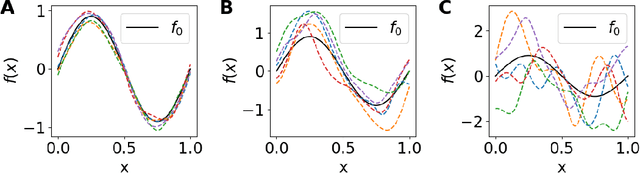
Discovering governing equations of a physical system, represented by partial differential equations (PDEs), from data is a central challenge in a variety of areas of science and engineering. Current methods require either some prior knowledge (e.g., candidate PDE terms) to discover the PDE form, or a large dataset to learn a surrogate model of the PDE solution operator. Here, we propose the first learning method that only needs one PDE solution, i.e., one-shot learning. We first decompose the entire computational domain into small domains, where we learn a local solution operator, and then find the coupled solution via a fixed-point iteration. We demonstrate the effectiveness of our method on different PDEs, and our method exhibits a strong generalization property.

A Latent space solver for PDE generalization

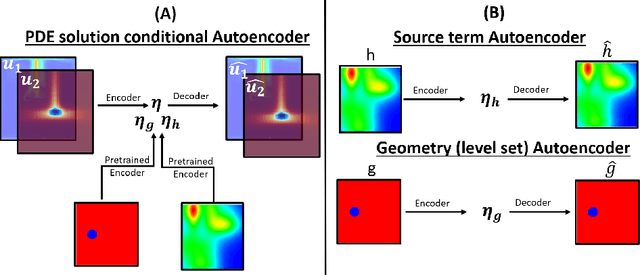
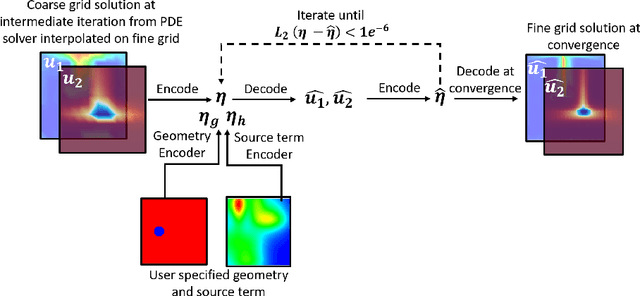
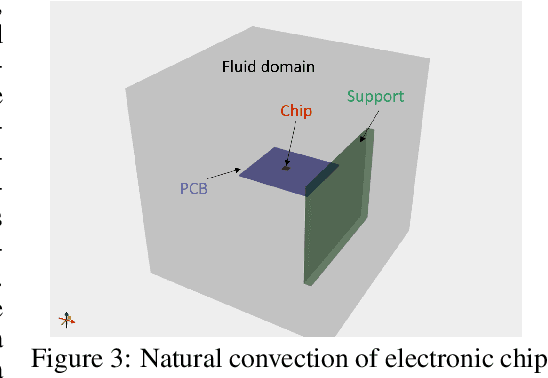
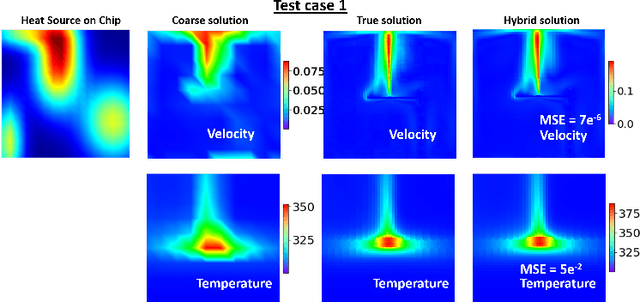
In this work we propose a hybrid solver to solve partial differential equation (PDE)s in the latent space. The solver uses an iterative inferencing strategy combined with solution initialization to improve generalization of PDE solutions. The solver is tested on an engineering case and the results show that it can generalize well to several PDE conditions.

Active Deep Learning on Entity Resolution by Risk Sampling

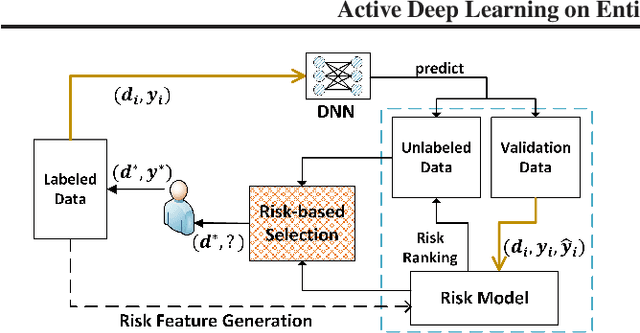
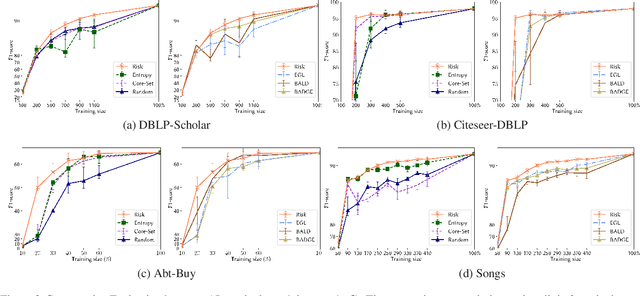
While the state-of-the-art performance on entity resolution (ER) has been achieved by deep learning, its effectiveness depends on large quantities of accurately labeled training data. To alleviate the data labeling burden, Active Learning (AL) presents itself as a feasible solution that focuses on data deemed useful for model training. Building upon the recent advances in risk analysis for ER, which can provide a more refined estimate on label misprediction risk than the simpler classifier outputs, we propose a novel AL approach of risk sampling for ER. Risk sampling leverages misprediction risk estimation for active instance selection. Based on the core-set characterization for AL, we theoretically derive an optimization model which aims to minimize core-set loss with non-uniform Lipschitz continuity. Since the defined weighted K-medoids problem is NP-hard, we then present an efficient heuristic algorithm. Finally, we empirically verify the efficacy of the proposed approach on real data by a comparative study. Our extensive experiments have shown that it outperforms the existing alternatives by considerable margins. Using ER as a test case, we demonstrate that risk sampling is a promising approach potentially applicable to other challenging classification tasks.

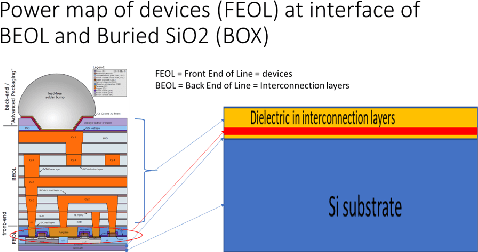
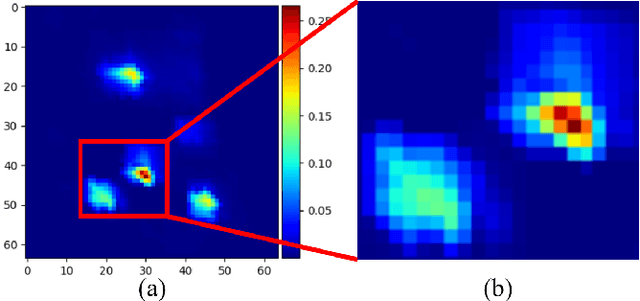
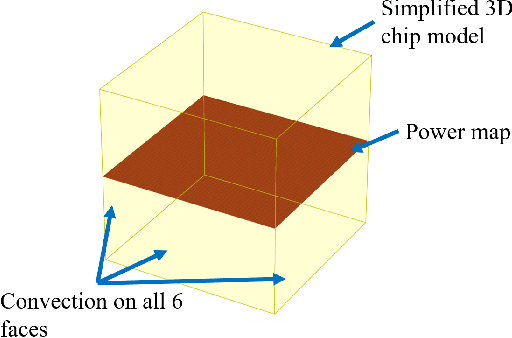
An unsupervised learning approach to solving heat equations on chip based on Auto Encoder and Image Gradient

Solving heat transfer equations on chip becomes very critical in the upcoming 5G and AI chip-package-systems. However, batches of simulations have to be performed for data driven supervised machine learning models. Data driven methods are data hungry, to address this, Physics Informed Neural Networks (PINN) have been proposed. However, vanilla PINN models solve one fixed heat equation at a time, so the models have to be retrained for heat equations with different source terms. Additionally, issues related to multi-objective optimization have to be resolved while using PINN to minimize the PDE residual, satisfy boundary conditions and fit the observed data etc. Therefore, this paper investigates an unsupervised learning approach for solving heat transfer equations on chip without using solution data and generalizing the trained network for predicting solutions for heat equations with unseen source terms. Specifically, a hybrid framework of Auto Encoder (AE) and Image Gradient (IG) based network is designed. The AE is used to encode different source terms of the heat equations. The IG based network implements a second order central difference algorithm for structured grids and minimizes the PDE residual. The effectiveness of the designed network is evaluated by solving heat equations for various use cases. It is proved that with limited number of source terms to train the AE network, the framework can not only solve the given heat transfer problems with a single training process, but also make reasonable predictions for unseen cases (heat equations with new source terms) without retraining.