One-shot learning for solution operators of partial differential equations

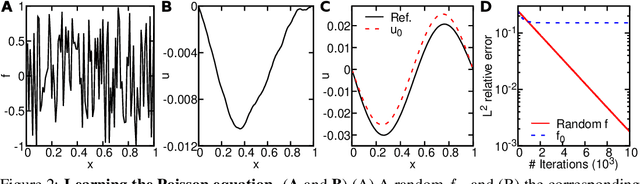
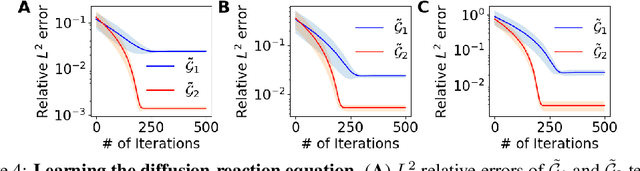
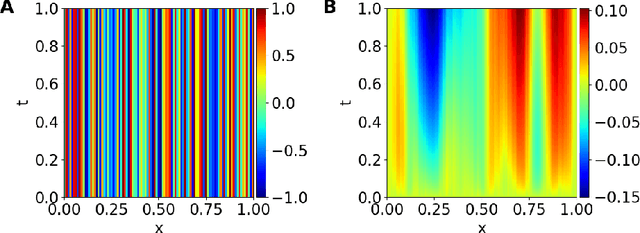
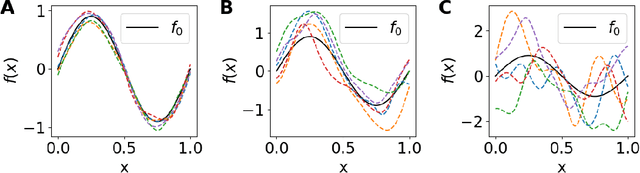
Discovering governing equations of a physical system, represented by partial differential equations (PDEs), from data is a central challenge in a variety of areas of science and engineering. Current methods require either some prior knowledge (e.g., candidate PDE terms) to discover the PDE form, or a large dataset to learn a surrogate model of the PDE solution operator. Here, we propose the first learning method that only needs one PDE solution, i.e., one-shot learning. We first decompose the entire computational domain into small domains, where we learn a local solution operator, and then find the coupled solution via a fixed-point iteration. We demonstrate the effectiveness of our method on different PDEs, and our method exhibits a strong generalization property.