Gustavo Camps-Valls
Nonlinearities and Adaptation of Color Vision from Sequential Principal Curves Analysis
Jan 31, 2016Abstract:Mechanisms of human color vision are characterized by two phenomenological aspects: the system is nonlinear and adaptive to changing environments. Conventional attempts to derive these features from statistics use separate arguments for each aspect. The few statistical approaches that do consider both phenomena simultaneously follow parametric formulations based on empirical models. Therefore, it may be argued that the behavior does not come directly from the color statistics but from the convenient functional form adopted. In addition, many times the whole statistical analysis is based on simplified databases that disregard relevant physical effects in the input signal, as for instance by assuming flat Lambertian surfaces. Here we address the simultaneous statistical explanation of (i) the nonlinear behavior of achromatic and chromatic mechanisms in a fixed adaptation state, and (ii) the change of such behavior. Both phenomena emerge directly from the samples through a single data-driven method: the Sequential Principal Curves Analysis (SPCA) with local metric. SPCA is a new manifold learning technique to derive a set of sensors adapted to the manifold using different optimality criteria. A new database of colorimetrically calibrated images of natural objects under these illuminants was collected. The results obtained by applying SPCA show that the psychophysical behavior on color discrimination thresholds, discount of the illuminant and corresponding pairs in asymmetric color matching, emerge directly from realistic data regularities assuming no a priori functional form. These results provide stronger evidence for the hypothesis of a statistically driven organization of color sensors. Moreover, the obtained results suggest that color perception at this low abstraction level may be guided by an error minimization strategy rather than by the information maximization principle.
Iterative Gaussianization: from ICA to Random Rotations
Jan 31, 2016


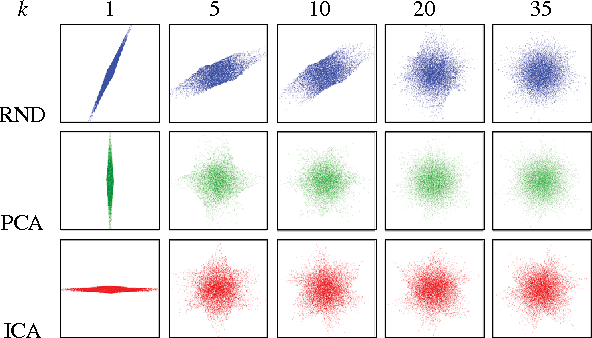
Abstract:Most signal processing problems involve the challenging task of multidimensional probability density function (PDF) estimation. In this work, we propose a solution to this problem by using a family of Rotation-based Iterative Gaussianization (RBIG) transforms. The general framework consists of the sequential application of a univariate marginal Gaussianization transform followed by an orthonormal transform. The proposed procedure looks for differentiable transforms to a known PDF so that the unknown PDF can be estimated at any point of the original domain. In particular, we aim at a zero mean unit covariance Gaussian for convenience. RBIG is formally similar to classical iterative Projection Pursuit (PP) algorithms. However, we show that, unlike in PP methods, the particular class of rotations used has no special qualitative relevance in this context, since looking for interestingness is not a critical issue for PDF estimation. The key difference is that our approach focuses on the univariate part (marginal Gaussianization) of the problem rather than on the multivariate part (rotation). This difference implies that one may select the most convenient rotation suited to each practical application. The differentiability, invertibility and convergence of RBIG are theoretically and experimentally analyzed. Relation to other methods, such as Radial Gaussianization (RG), one-class support vector domain description (SVDD), and deep neural networks (DNN) is also pointed out. The practical performance of RBIG is successfully illustrated in a number of multidimensional problems such as image synthesis, classification, denoising, and multi-information estimation.
Image Denoising with Kernels based on Natural Image Relations
Jan 31, 2016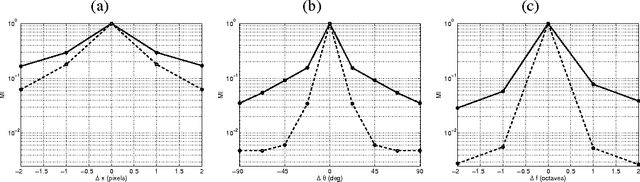
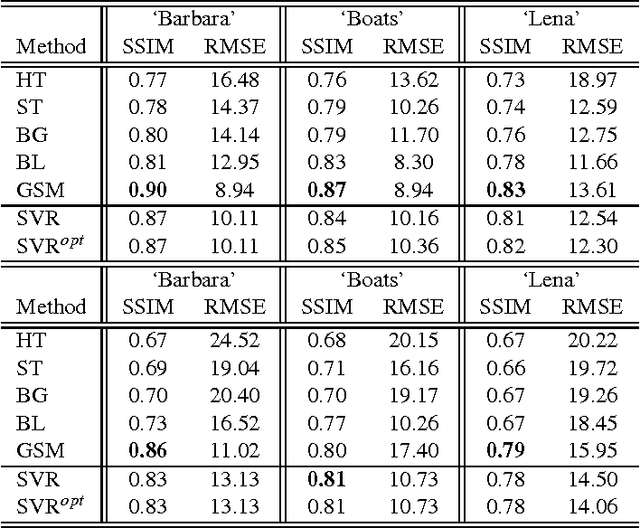
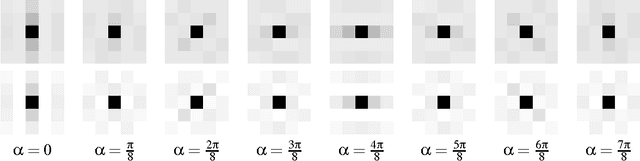
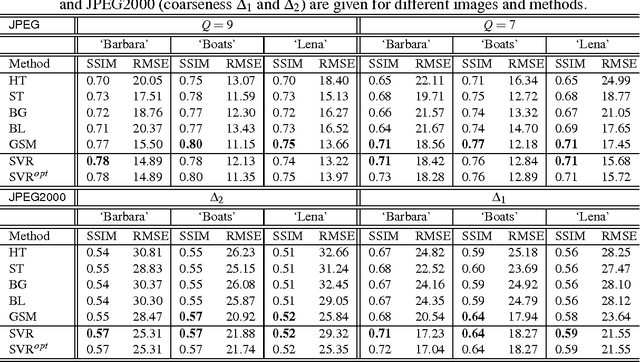
Abstract:A successful class of image denoising methods is based on Bayesian approaches working in wavelet representations. However, analytical estimates can be obtained only for particular combinations of analytical models of signal and noise, thus precluding its straightforward extension to deal with other arbitrary noise sources. In this paper, we propose an alternative non-explicit way to take into account the relations among natural image wavelet coefficients for denoising: we use support vector regression (SVR) in the wavelet domain to enforce these relations in the estimated signal. Since relations among the coefficients are specific to the signal, the regularization property of SVR is exploited to remove the noise, which does not share this feature. The specific signal relations are encoded in an anisotropic kernel obtained from mutual information measures computed on a representative image database. Training considers minimizing the Kullback-Leibler divergence (KLD) between the estimated and actual probability functions of signal and noise in order to enforce similarity. Due to its non-parametric nature, the method can eventually cope with different noise sources without the need of an explicit re-formulation, as it is strictly necessary under parametric Bayesian formalisms. Results under several noise levels and noise sources show that: (1) the proposed method outperforms conventional wavelet methods that assume coefficient independence, (2) it is similar to state-of-the-art methods that do explicitly include these relations when the noise source is Gaussian, and (3) it gives better numerical and visual performance when more complex, realistic noise sources are considered. Therefore, the proposed machine learning approach can be seen as a more flexible (model-free) alternative to the explicit description of wavelet coefficient relations for image denoising.
A Unified SVM Framework for Signal Estimation
Nov 21, 2013
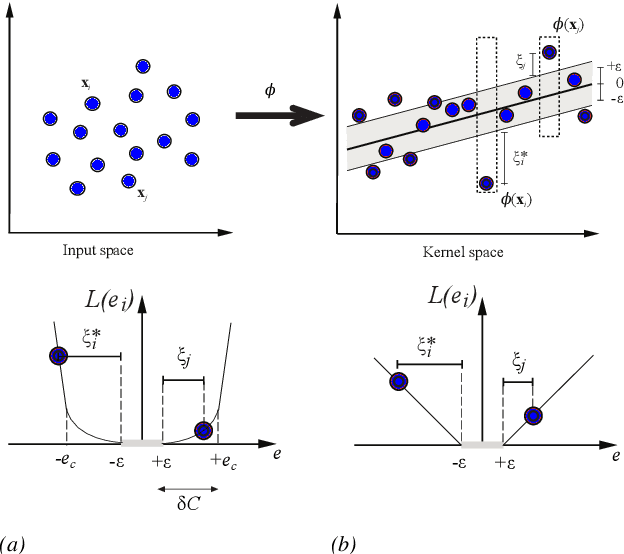

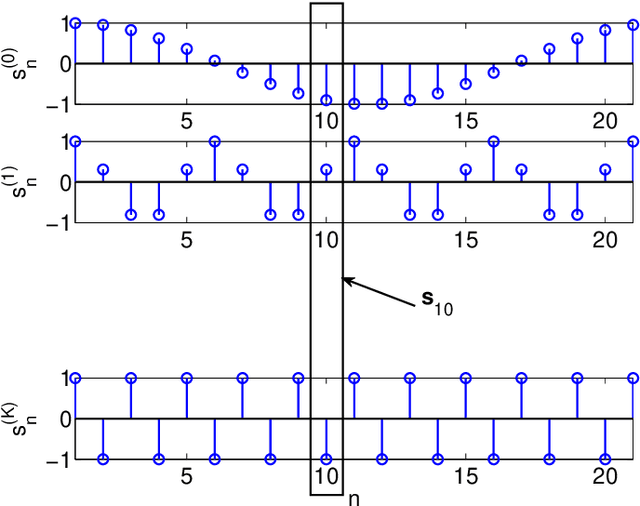
Abstract:This paper presents a unified framework to tackle estimation problems in Digital Signal Processing (DSP) using Support Vector Machines (SVMs). The use of SVMs in estimation problems has been traditionally limited to its mere use as a black-box model. Noting such limitations in the literature, we take advantage of several properties of Mercer's kernels and functional analysis to develop a family of SVM methods for estimation in DSP. Three types of signal model equations are analyzed. First, when a specific time-signal structure is assumed to model the underlying system that generated the data, the linear signal model (so called Primal Signal Model formulation) is first stated and analyzed. Then, non-linear versions of the signal structure can be readily developed by following two different approaches. On the one hand, the signal model equation is written in reproducing kernel Hilbert spaces (RKHS) using the well-known RKHS Signal Model formulation, and Mercer's kernels are readily used in SVM non-linear algorithms. On the other hand, in the alternative and not so common Dual Signal Model formulation, a signal expansion is made by using an auxiliary signal model equation given by a non-linear regression of each time instant in the observed time series. These building blocks can be used to generate different novel SVM-based methods for problems of signal estimation, and we deal with several of the most important ones in DSP. We illustrate the usefulness of this methodology by defining SVM algorithms for linear and non-linear system identification, spectral analysis, nonuniform interpolation, sparse deconvolution, and array processing. The performance of the developed SVM methods is compared to standard approaches in all these settings. The experimental results illustrate the generality, simplicity, and capabilities of the proposed SVM framework for DSP.
Advances in Hyperspectral Image Classification: Earth monitoring with statistical learning methods
Oct 18, 2013
Abstract:Hyperspectral images show similar statistical properties to natural grayscale or color photographic images. However, the classification of hyperspectral images is more challenging because of the very high dimensionality of the pixels and the small number of labeled examples typically available for learning. These peculiarities lead to particular signal processing problems, mainly characterized by indetermination and complex manifolds. The framework of statistical learning has gained popularity in the last decade. New methods have been presented to account for the spatial homogeneity of images, to include user's interaction via active learning, to take advantage of the manifold structure with semisupervised learning, to extract and encode invariances, or to adapt classifiers and image representations to unseen yet similar scenes. This tutuorial reviews the main advances for hyperspectral remote sensing image classification through illustrative examples.
Kernel Multivariate Analysis Framework for Supervised Subspace Learning: A Tutorial on Linear and Kernel Multivariate Methods
Oct 18, 2013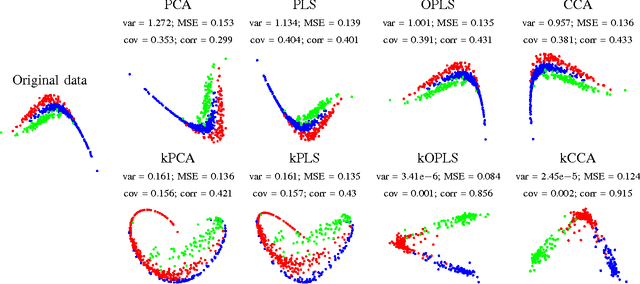
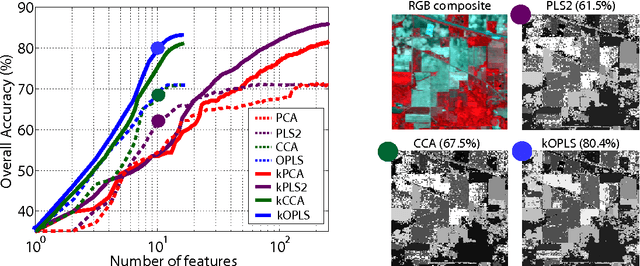
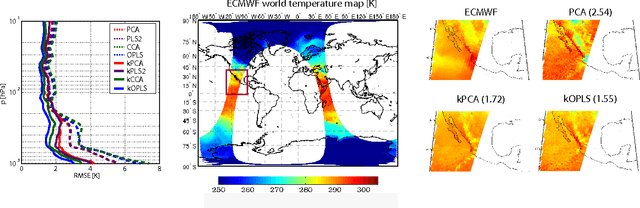
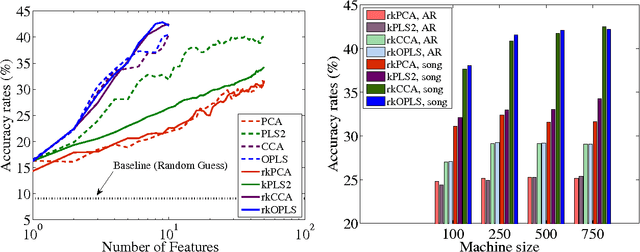
Abstract:Feature extraction and dimensionality reduction are important tasks in many fields of science dealing with signal processing and analysis. The relevance of these techniques is increasing as current sensory devices are developed with ever higher resolution, and problems involving multimodal data sources become more common. A plethora of feature extraction methods are available in the literature collectively grouped under the field of Multivariate Analysis (MVA). This paper provides a uniform treatment of several methods: Principal Component Analysis (PCA), Partial Least Squares (PLS), Canonical Correlation Analysis (CCA) and Orthonormalized PLS (OPLS), as well as their non-linear extensions derived by means of the theory of reproducing kernel Hilbert spaces. We also review their connections to other methods for classification and statistical dependence estimation, and introduce some recent developments to deal with the extreme cases of large-scale and low-sized problems. To illustrate the wide applicability of these methods in both classification and regression problems, we analyze their performance in a benchmark of publicly available data sets, and pay special attention to specific real applications involving audio processing for music genre prediction and hyperspectral satellite images for Earth and climate monitoring.
On the Suitable Domain for SVM Training in Image Coding
Oct 18, 2013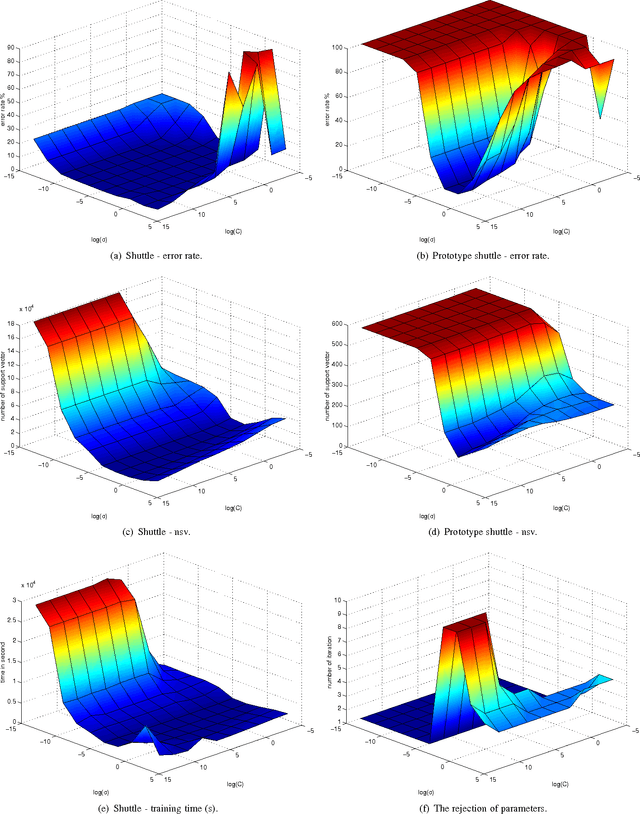
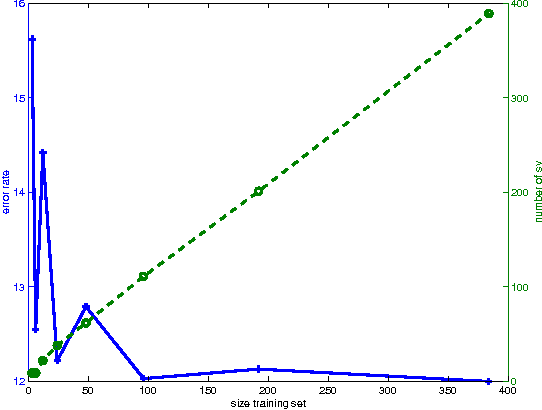

Abstract:Conventional SVM-based image coding methods are founded on independently restricting the distortion in every image coefficient at some particular image representation. Geometrically, this implies allowing arbitrary signal distortions in an $n$-dimensional rectangle defined by the $\varepsilon$-insensitivity zone in each dimension of the selected image representation domain. Unfortunately, not every image representation domain is well-suited for such a simple, scalar-wise, approach because statistical and/or perceptual interactions between the coefficients may exist. These interactions imply that scalar approaches may induce distortions that do not follow the image statistics and/or are perceptually annoying. Taking into account these relations would imply using non-rectangular $\varepsilon$-insensitivity regions (allowing coupled distortions in different coefficients), which is beyond the conventional SVM formulation. In this paper, we report a condition on the suitable domain for developing efficient SVM image coding schemes. We analytically demonstrate that no linear domain fulfills this condition because of the statistical and perceptual inter-coefficient relations that exist in these domains. This theoretical result is experimentally confirmed by comparing SVM learning in previously reported linear domains and in a recently proposed non-linear perceptual domain that simultaneously reduces the statistical and perceptual relations (so it is closer to fulfilling the proposed condition). These results highlight the relevance of an appropriate choice of the image representation before SVM learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge