Kaare Brandt Petersen
Kernel Multivariate Analysis Framework for Supervised Subspace Learning: A Tutorial on Linear and Kernel Multivariate Methods
Oct 18, 2013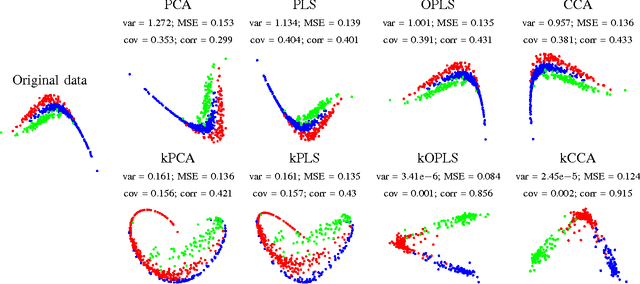
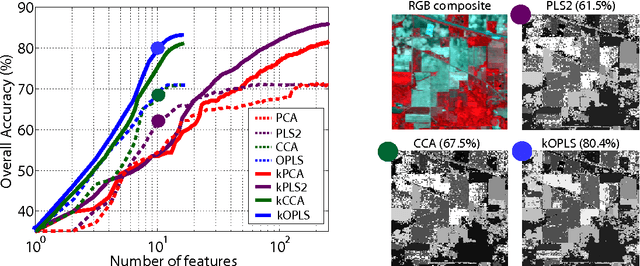
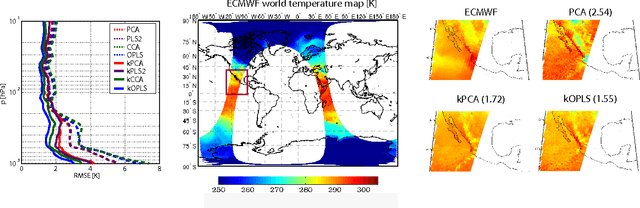
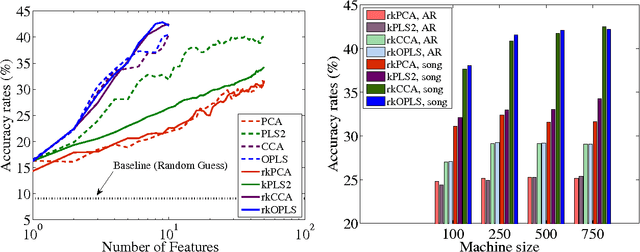
Abstract:Feature extraction and dimensionality reduction are important tasks in many fields of science dealing with signal processing and analysis. The relevance of these techniques is increasing as current sensory devices are developed with ever higher resolution, and problems involving multimodal data sources become more common. A plethora of feature extraction methods are available in the literature collectively grouped under the field of Multivariate Analysis (MVA). This paper provides a uniform treatment of several methods: Principal Component Analysis (PCA), Partial Least Squares (PLS), Canonical Correlation Analysis (CCA) and Orthonormalized PLS (OPLS), as well as their non-linear extensions derived by means of the theory of reproducing kernel Hilbert spaces. We also review their connections to other methods for classification and statistical dependence estimation, and introduce some recent developments to deal with the extreme cases of large-scale and low-sized problems. To illustrate the wide applicability of these methods in both classification and regression problems, we analyze their performance in a benchmark of publicly available data sets, and pay special attention to specific real applications involving audio processing for music genre prediction and hyperspectral satellite images for Earth and climate monitoring.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge