Multivariate Feature Selection and Autoencoder Embeddings of Ovarian Cancer Clinical and Genetic Data

This study explores a data-driven approach to discovering novel clinical and genetic markers in ovarian cancer (OC). Two main analyses were performed: (1) a nonlinear examination of an OC dataset using autoencoders, which compress data into a 3-dimensional latent space to detect potential intrinsic separability between platinum-sensitive and platinum-resistant groups; and (2) an adaptation of the informative variable identifier (IVI) to determine which features (clinical or genetic) are most relevant to disease progression. In the autoencoder analysis, a clearer pattern emerged when using clinical features and the combination of clinical and genetic data, indicating that disease progression groups can be distinguished more effectively after supervised fine tuning. For genetic data alone, this separability was less apparent but became more pronounced with a supervised approach. Using the IVI-based feature selection, key clinical variables (such as type of surgery and neoadjuvant chemotherapy) and certain gene mutations showed strong relevance, along with low-risk genetic factors. These findings highlight the strength of combining machine learning tools (autoencoders) with feature selection methods (IVI) to gain insights into ovarian cancer progression. They also underscore the potential for identifying new biomarkers that integrate clinical and genomic indicators, ultimately contributing to improved patient stratification and personalized treatment strategies.

A Unified SVM Framework for Signal Estimation

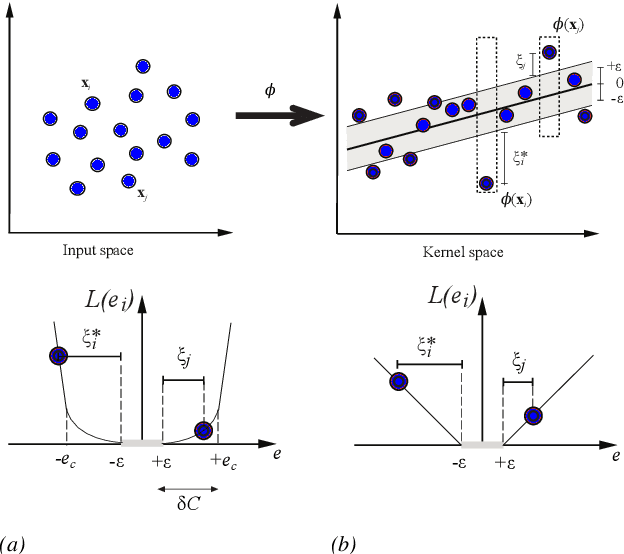
This paper presents a unified framework to tackle estimation problems in Digital Signal Processing (DSP) using Support Vector Machines (SVMs). The use of SVMs in estimation problems has been traditionally limited to its mere use as a black-box model. Noting such limitations in the literature, we take advantage of several properties of Mercer's kernels and functional analysis to develop a family of SVM methods for estimation in DSP. Three types of signal model equations are analyzed. First, when a specific time-signal structure is assumed to model the underlying system that generated the data, the linear signal model (so called Primal Signal Model formulation) is first stated and analyzed. Then, non-linear versions of the signal structure can be readily developed by following two different approaches. On the one hand, the signal model equation is written in reproducing kernel Hilbert spaces (RKHS) using the well-known RKHS Signal Model formulation, and Mercer's kernels are readily used in SVM non-linear algorithms. On the other hand, in the alternative and not so common Dual Signal Model formulation, a signal expansion is made by using an auxiliary signal model equation given by a non-linear regression of each time instant in the observed time series. These building blocks can be used to generate different novel SVM-based methods for problems of signal estimation, and we deal with several of the most important ones in DSP. We illustrate the usefulness of this methodology by defining SVM algorithms for linear and non-linear system identification, spectral analysis, nonuniform interpolation, sparse deconvolution, and array processing. The performance of the developed SVM methods is compared to standard approaches in all these settings. The experimental results illustrate the generality, simplicity, and capabilities of the proposed SVM framework for DSP.