Multivariate Feature Selection and Autoencoder Embeddings of Ovarian Cancer Clinical and Genetic Data

This study explores a data-driven approach to discovering novel clinical and genetic markers in ovarian cancer (OC). Two main analyses were performed: (1) a nonlinear examination of an OC dataset using autoencoders, which compress data into a 3-dimensional latent space to detect potential intrinsic separability between platinum-sensitive and platinum-resistant groups; and (2) an adaptation of the informative variable identifier (IVI) to determine which features (clinical or genetic) are most relevant to disease progression. In the autoencoder analysis, a clearer pattern emerged when using clinical features and the combination of clinical and genetic data, indicating that disease progression groups can be distinguished more effectively after supervised fine tuning. For genetic data alone, this separability was less apparent but became more pronounced with a supervised approach. Using the IVI-based feature selection, key clinical variables (such as type of surgery and neoadjuvant chemotherapy) and certain gene mutations showed strong relevance, along with low-risk genetic factors. These findings highlight the strength of combining machine learning tools (autoencoders) with feature selection methods (IVI) to gain insights into ovarian cancer progression. They also underscore the potential for identifying new biomarkers that integrate clinical and genomic indicators, ultimately contributing to improved patient stratification and personalized treatment strategies.

Nonnegative OPLS for Supervised Design of Filter Banks: Application to Image and Audio Feature Extraction

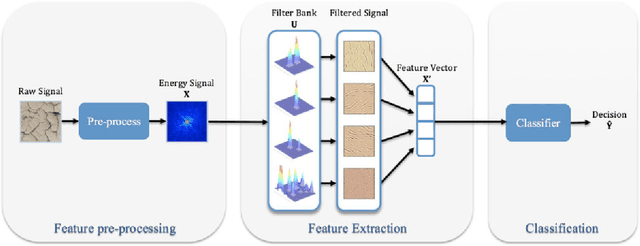
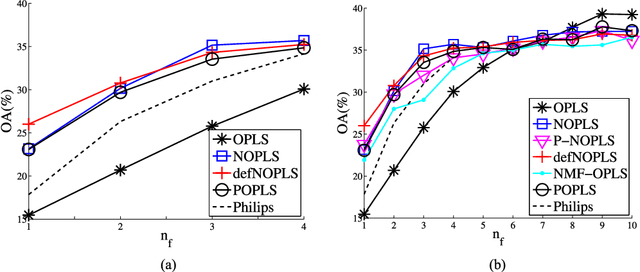
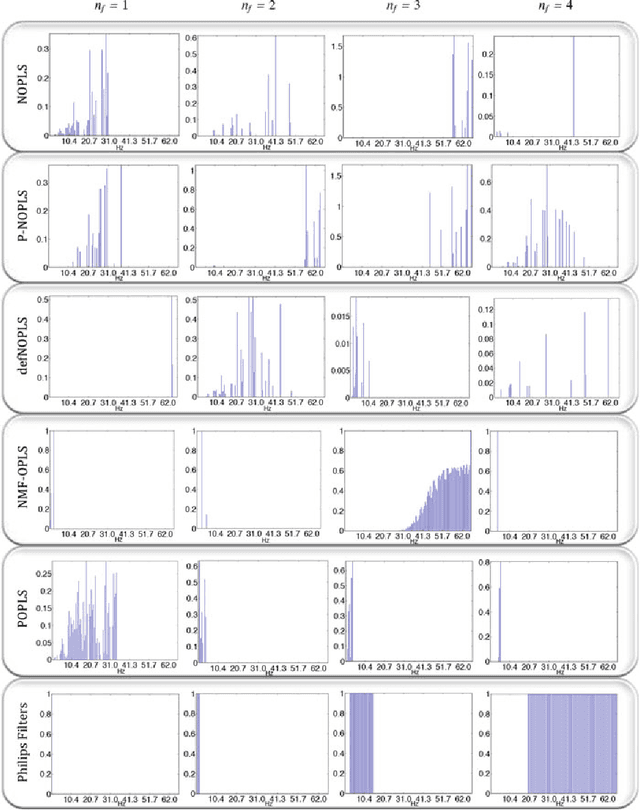
Audio or visual data analysis tasks usually have to deal with high-dimensional and nonnegative signals. However, most data analysis methods suffer from overfitting and numerical problems when data have more than a few dimensions needing a dimensionality reduction preprocessing. Moreover, interpretability about how and why filters work for audio or visual applications is a desired property, especially when energy or spectral signals are involved. In these cases, due to the nature of these signals, the nonnegativity of the filter weights is a desired property to better understand its working. Because of these two necessities, we propose different methods to reduce the dimensionality of data while the nonnegativity and interpretability of the solution are assured. In particular, we propose a generalized methodology to design filter banks in a supervised way for applications dealing with nonnegative data, and we explore different ways of solving the proposed objective function consisting of a nonnegative version of the orthonormalized partial least-squares method. We analyze the discriminative power of the features obtained with the proposed methods for two different and widely studied applications: texture and music genre classification. Furthermore, we compare the filter banks achieved by our methods with other state-of-the-art methods specifically designed for feature extraction.

Regularized Multivariate Analysis Framework for Interpretable High-Dimensional Variable Selection

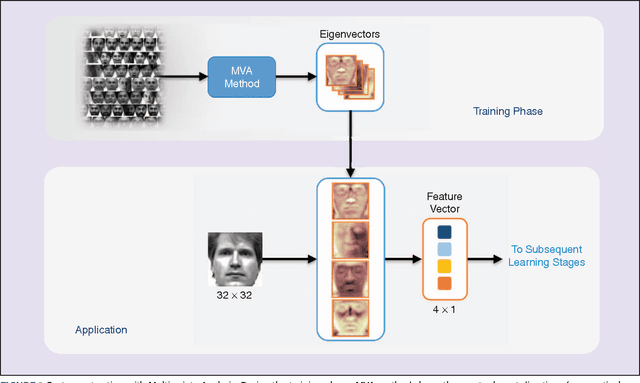
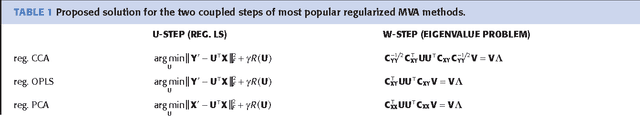
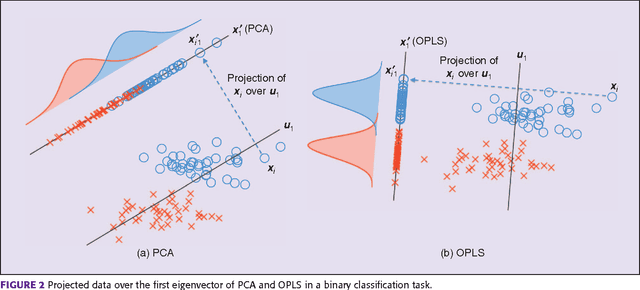
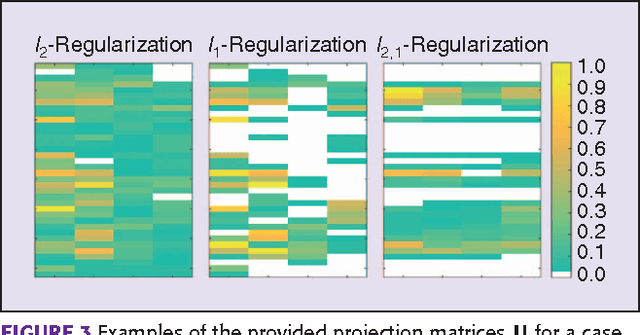
Multivariate Analysis (MVA) comprises a family of well-known methods for feature extraction which exploit correlations among input variables representing the data. One important property that is enjoyed by most such methods is uncorrelation among the extracted features. Recently, regularized versions of MVA methods have appeared in the literature, mainly with the goal to gain interpretability of the solution. In these cases, the solutions can no longer be obtained in a closed manner, and more complex optimization methods that rely on the iteration of two steps are frequently used. This paper recurs to an alternative approach to solve efficiently this iterative problem. The main novelty of this approach lies in preserving several properties of the original methods, most notably the uncorrelation of the extracted features. Under this framework, we propose a novel method that takes advantage of the l-21 norm to perform variable selection during the feature extraction process. Experimental results over different problems corroborate the advantages of the proposed formulation in comparison to state of the art formulations.

Why (and How) Avoid Orthogonal Procrustes in Regularized Multivariate Analysis

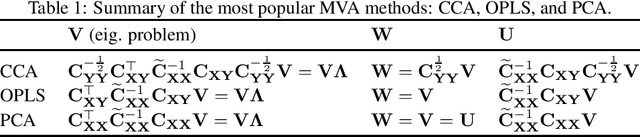
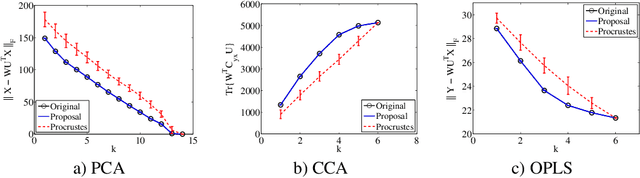
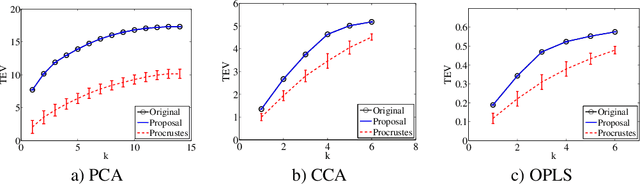
Multivariate Analysis (MVA) comprises a family of well-known methods for feature extraction that exploit correlations among input variables of the data representation. One important property that is enjoyed by most such methods is uncorrelation among the extracted features. Recently, regularized versions of MVA methods have appeared in the literature, mainly with the goal to gain interpretability of the solution. In these cases, the solutions can no longer be obtained in a closed manner, and it is frequent to recur to the iteration of two steps, one of them being an orthogonal Procrustes problem. This letter shows that the Procrustes solution is not optimal from the perspective of the overall MVA method, and proposes an alternative approach based on the solution of an eigenvalue problem. Our method ensures the preservation of several properties of the original methods, most notably the uncorrelation of the extracted features, as demonstrated theoretically and through a collection of selected experiments.