Why (and How) Avoid Orthogonal Procrustes in Regularized Multivariate Analysis
Paper and Code
Sep 19, 2016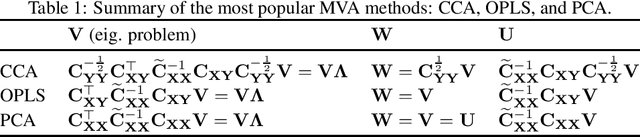
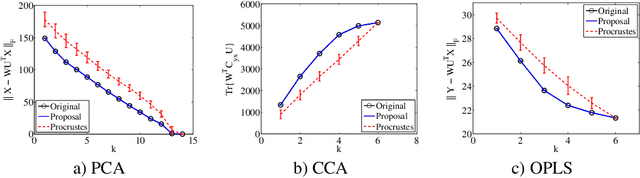

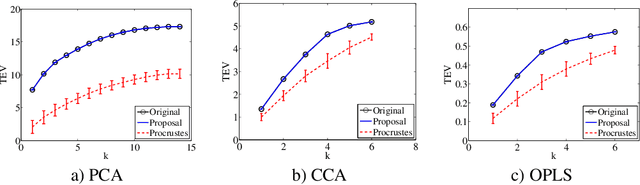
Multivariate Analysis (MVA) comprises a family of well-known methods for feature extraction that exploit correlations among input variables of the data representation. One important property that is enjoyed by most such methods is uncorrelation among the extracted features. Recently, regularized versions of MVA methods have appeared in the literature, mainly with the goal to gain interpretability of the solution. In these cases, the solutions can no longer be obtained in a closed manner, and it is frequent to recur to the iteration of two steps, one of them being an orthogonal Procrustes problem. This letter shows that the Procrustes solution is not optimal from the perspective of the overall MVA method, and proposes an alternative approach based on the solution of an eigenvalue problem. Our method ensures the preservation of several properties of the original methods, most notably the uncorrelation of the extracted features, as demonstrated theoretically and through a collection of selected experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge