A Novel Sparse Sum and Difference Co-Array With Low Redundancy and Enhanced DOF for Non-Circular Signals

Array structures based on the sum and difference co-arrays provide more degrees of freedom (DOF). However, since the growth of DOF is limited by a single case of sum and difference co-arrays, the paper aims to design a sparse linear array (SLA) with higher DOF via exploring different cases of second-order cumulants. We present a mathematical framework based on second-order cumulant to devise a second-order extended co-array (SO-ECA) and define the redundancy of SO-ECA. Based on SO-ECA, a novel array is proposed, namely low redundancy sum and difference array (LR-SDA), which can provide closed-form expressions for the sensor positions and enhance DOF in order to resolve more signal sources in the direction of arrival (DOA) estimation of non-circular (NC) signals. For LR-SDA, the maximum DOF under the given number of total physical sensors can be derived and the SO-ECA of LR-SDA is hole-free. Further, the corresponding necessary and sufficient conditions of signal reconstruction for LR-SDA are derived. Additionally, the redundancy and weight function of LR-SDA are defined, and the lower band of the redundancy for LR-SDA is derived. The proposed LR-SDA achieves higher DOF and lower redundancy than those of existing DCAs designed based on sum and difference co-arrays. Numerical simulations are conducted to verify the superiority of LR-SDA on DOA estimation performance and enhanced DOF over other existing DCAs.

FOGNA: An effective Sum-Difference Co-Array Design Based on Fourth-Order Cumulants

Array structures based on the fourth-order difference co-array (FODCA) provide more degrees of freedom (DOF). However, since the growth of DOF is limited by a single case of fourth-order cumulant in FODCA, this paper aims to design a sparse linear array (SLA) with higher DOF via exploring different cases of fourth-order cumulants. This paper presents a mathematical framework based on fourth-order cumulant to devise a fourth-order extend co-array (FOECA), which is equivalent to FODCA. A novel SLA, namely fourth-order generalized nested array (FOGNA), is proposed based on FOECA to provide closed-form expressions for the sensor locations and enhance DOF to resolve more signal sources in direction of arrival (DOA) estimation. FOGNA is consisted of three subarrays, where the first is a concatenated nested array and the other two subarrays are SLA with big inter-spacing between sensors. When the total physical sensors of FOGNA are given, the number of sensors in each subarray is determined by the designed method, which can obtain the maximum DOF under the proposed array structure and derive closed-form expressions for the sensor locations of FOGNA. The proposed array structure not only achieves higher DOF than those of existing FODCAs but also reduces mutual coupling effects. Numerical simulations are conducted to verify the superiority of FOGNA on DOA estimation performance and enhanced DOF over other existing FODCAs.

Parametric Primitive Analysis of CAD Sketches with Vision Transformer

The design and analysis of Computer-Aided Design (CAD) sketches play a crucial role in industrial product design, primarily involving CAD primitives and their inter-primitive constraints. To address challenges related to error accumulation in autoregressive models and the complexities associated with self-supervised model design for this task, we propose a two-stage network framework. This framework consists of a primitive network and a constraint network, transforming the sketch analysis task into a set prediction problem to enhance the effective handling of primitives and constraints. By decoupling target types from parameters, the model gains increased flexibility and optimization while reducing complexity. Additionally, the constraint network incorporates a pointer module to explicitly indicate the relationship between constraint parameters and primitive indices, enhancing interpretability and performance. Qualitative and quantitative analyses on two publicly available datasets demonstrate the superiority of this method.

Edge Preserving Implicit Surface Representation of Point Clouds

Learning implicit surface directly from raw data recently has become a very attractive representation method for 3D reconstruction tasks due to its excellent performance. However, as the raw data quality deteriorates, the implicit functions often lead to unsatisfactory reconstruction results. To this end, we propose a novel edge-preserving implicit surface reconstruction method, which mainly consists of a differentiable Laplican regularizer and a dynamic edge sampling strategy. Among them, the differential Laplican regularizer can effectively alleviate the implicit surface unsmoothness caused by the point cloud quality deteriorates; Meanwhile, in order to reduce the excessive smoothing at the edge regions of implicit suface, we proposed a dynamic edge extract strategy for sampling near the sharp edge of point cloud, which can effectively avoid the Laplacian regularizer from smoothing all regions. Finally, we combine them with a simple regularization term for robust implicit surface reconstruction. Compared with the state-of-the-art methods, experimental results show that our method significantly improves the quality of 3D reconstruction results. Moreover, we demonstrate through several experiments that our method can be conveniently and effectively applied to some point cloud analysis tasks, including point cloud edge feature extraction, normal estimation,etc.

PCB-RandNet: Rethinking Random Sampling for LIDAR Semantic Segmentation in Autonomous Driving Scene

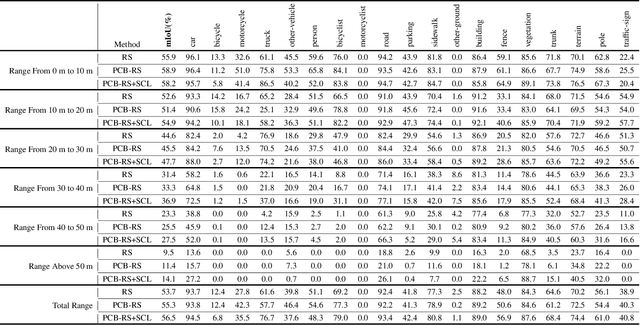
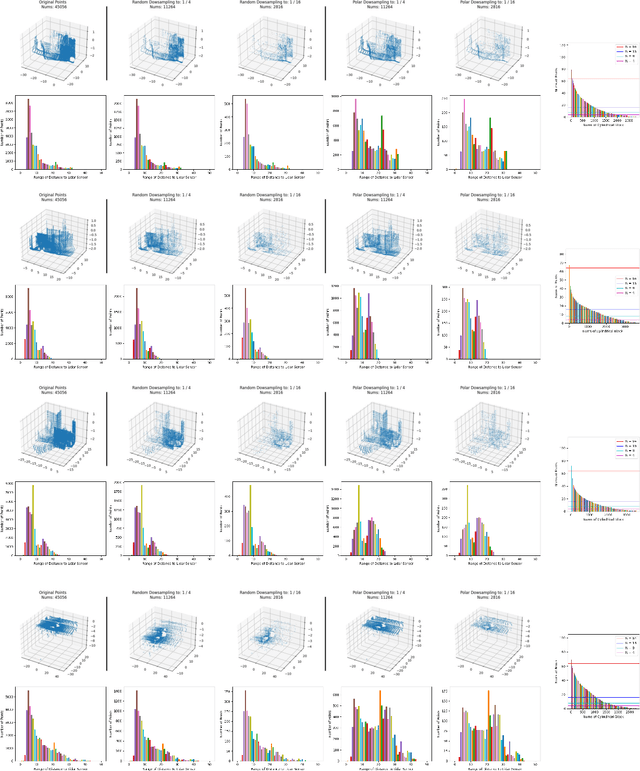
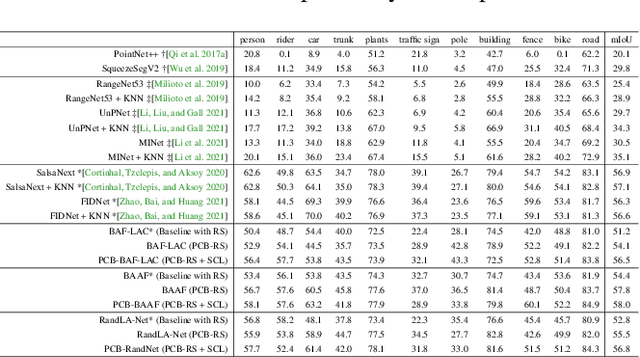
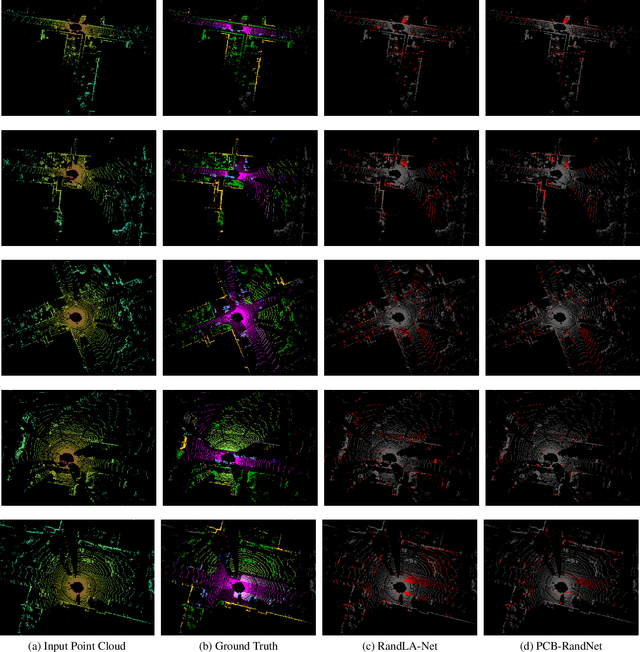
Fast and efficient semantic segmentation of large-scale LiDAR point clouds is a fundamental problem in autonomous driving. To achieve this goal, the existing point-based methods mainly choose to adopt Random Sampling strategy to process large-scale point clouds. However, our quantative and qualitative studies have found that Random Sampling may be less suitable for the autonomous driving scenario, since the LiDAR points follow an uneven or even long-tailed distribution across the space, which prevents the model from capturing sufficient information from points in different distance ranges and reduces the model's learning capability. To alleviate this problem, we propose a new Polar Cylinder Balanced Random Sampling method that enables the downsampled point clouds to maintain a more balanced distribution and improve the segmentation performance under different spatial distributions. In addition, a sampling consistency loss is introduced to further improve the segmentation performance and reduce the model's variance under different sampling methods. Extensive experiments confirm that our approach produces excellent performance on both SemanticKITTI and SemanticPOSS benchmarks, achieving a 2.8% and 4.0% improvement, respectively.

LKD-Net: Large Kernel Convolution Network for Single Image Dehazing

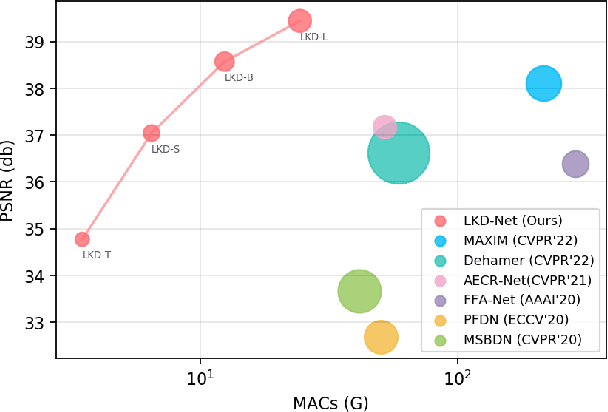
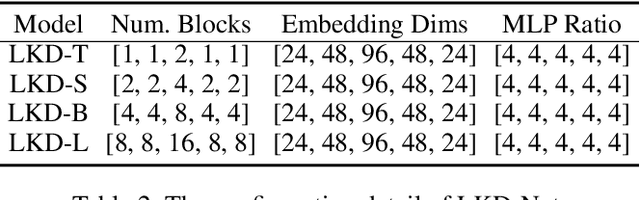
The deep convolutional neural networks (CNNs)-based single image dehazing methods have achieved significant success. The previous methods are devoted to improving the network's performance by increasing the network's depth and width. The current methods focus on increasing the convolutional kernel size to enhance its performance by benefiting from the larger receptive field. However, directly increasing the size of the convolutional kernel introduces a massive amount of computational overhead and parameters. Thus, a novel Large Kernel Convolution Dehaze Block (LKD Block) consisting of the Decomposition deep-wise Large Kernel Convolution Block (DLKCB) and the Channel Enhanced Feed-forward Network (CEFN) is devised in this paper. The designed DLKCB can split the deep-wise large kernel convolution into a smaller depth-wise convolution and a depth-wise dilated convolution without introducing massive parameters and computational overhead. Meanwhile, the designed CEFN incorporates a channel attention mechanism into Feed-forward Network to exploit significant channels and enhance robustness. By combining multiple LKD Blocks and Up-Down sampling modules, the Large Kernel Convolution Dehaze Network (LKD-Net) is conducted. The evaluation results demonstrate the effectiveness of the designed DLKCB and CEFN, and our LKD-Net outperforms the state-of-the-art. On the SOTS indoor dataset, our LKD-Net dramatically outperforms the Transformer-based method Dehamer with only 1.79% #Param and 48.9% FLOPs. The source code of our LKD-Net is available at https://github.com/SWU-CS-MediaLab/LKD-Net.

Multiple Independent Subspace Clusterings

Multiple clustering aims at discovering diverse ways of organizing data into clusters. Despite the progress made, it's still a challenge for users to analyze and understand the distinctive structure of each output clustering. To ease this process, we consider diverse clusterings embedded in different subspaces, and analyze the embedding subspaces to shed light into the structure of each clustering. To this end, we provide a two-stage approach called MISC (Multiple Independent Subspace Clusterings). In the first stage, MISC uses independent subspace analysis to seek multiple and statistical independent (i.e. non-redundant) subspaces, and determines the number of subspaces via the minimum description length principle. In the second stage, to account for the intrinsic geometric structure of samples embedded in each subspace, MISC performs graph regularized semi-nonnegative matrix factorization to explore clusters. It additionally integrates the kernel trick into matrix factorization to handle non-linearly separable clusters. Experimental results on synthetic datasets show that MISC can find different interesting clusterings from the sought independent subspaces, and it also outperforms other related and competitive approaches on real-world datasets.