ORAgentBench: Can LLM Agents Solve Challenging Operations Research Tasks End to End?

Large language models are increasingly deployed as autonomous agents for multi-step tasks in executable environments, yet their ability to perform realistic operations research (OR) work remains unclear. Existing OR evaluations often decouple modeling from solving, rely on pre-formalized or text-only instances, and rarely test the full workflow from operational artifacts to validated decisions. In this work, we introduce ORAgentBench, an execution-grounded benchmark for evaluating autonomous agents on challenging end-to-end operations research tasks. It contains 107 human-reviewed tasks across diverse operational scenarios, each packaged in an isolated environment with a natural-language brief, multi-file data, configuration artifacts, and a required submission schema. Agents must write and run solution code, and their submissions are evaluated by hidden validators for schema validity, hard-constraint feasibility, and normalized objective quality. Experiments with fourteen frontier agent-model configurations show that current agents remain far from reliable OR practice. The best agent passes only 35.51% of all tasks and 20.59% of hard tasks, and many feasible submissions still fall below the required quality threshold. Failure analysis further shows that errors are dominated by strategic weaknesses, including missed operational rules, brittle formulations, weak feasible-solution construction, and insufficient solution improvement. OR-specific procedural skills increase hard-task feasibility, but do not reliably improve solution quality or pass rate. These results suggest that progress in OR agents requires moving beyond plausible optimization code toward dependable, high-quality operational decision-making.

Stochastic $k$-Submodular Bandits with Full Bandit Feedback

In this paper, we present the first sublinear $\alpha$-regret bounds for online $k$-submodular optimization problems with full-bandit feedback, where $\alpha$ is a corresponding offline approximation ratio. Specifically, we propose online algorithms for multiple $k$-submodular stochastic combinatorial multi-armed bandit problems, including (i) monotone functions and individual size constraints, (ii) monotone functions with matroid constraints, (iii) non-monotone functions with matroid constraints, (iv) non-monotone functions without constraints, and (v) monotone functions without constraints. We transform approximation algorithms for offline $k$-submodular maximization problems into online algorithms through the offline-to-online framework proposed by Nie et al. (2023a). A key contribution of our work is analyzing the robustness of the offline algorithms.

Hammer: Robust Function-Calling for On-Device Language Models via Function Masking

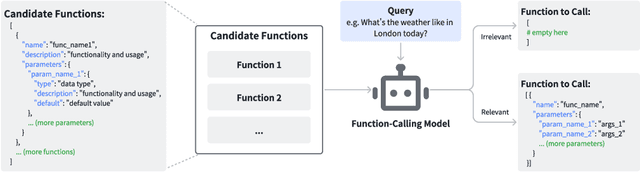
Large language models have demonstrated impressive value in performing as autonomous agents when equipped with external tools and API calls. Nonetheless, effectively harnessing their potential for executing complex tasks crucially relies on enhancements in their function calling capabilities. This paper identifies a critical gap in existing function calling models, where performance varies significantly across benchmarks, often due to being misled by specific naming conventions. To address such an issue, we introduce Hammer, a novel family of foundation models specifically engineered for on-device function calling. Hammer employs an augmented dataset that enhances models' sensitivity to irrelevant functions and incorporates function masking techniques to minimize misleading. Our empirical evaluations reveal that Hammer not only outperforms larger models but also demonstrates robust generalization across diverse benchmarks, achieving sota results. Our open source contributions include a specialized dataset for irrelevance detection, a tuning framework for enhanced generalization, and the Hammer models, establishing a new standard for function calling performance.

A Framework for Adapting Offline Algorithms to Solve Combinatorial Multi-Armed Bandit Problems with Bandit Feedback

We investigate the problem of stochastic, combinatorial multi-armed bandits where the learner only has access to bandit feedback and the reward function can be non-linear. We provide a general framework for adapting discrete offline approximation algorithms into sublinear $\alpha$-regret methods that only require bandit feedback, achieving $\mathcal{O}\left(T^\frac{2}{3}\log(T)^\frac{1}{3}\right)$ expected cumulative $\alpha$-regret dependence on the horizon $T$. The framework only requires the offline algorithms to be robust to small errors in function evaluation. The adaptation procedure does not even require explicit knowledge of the offline approximation algorithm -- the offline algorithm can be used as black box subroutine. To demonstrate the utility of the proposed framework, the proposed framework is applied to multiple problems in submodular maximization, adapting approximation algorithms for cardinality and for knapsack constraints. The new CMAB algorithms for knapsack constraints outperform a full-bandit method developed for the adversarial setting in experiments with real-world data.