On the Koopman-Based Generalization Bounds for Multi-Task Deep Learning

The paper establishes generalization bounds for multitask deep neural networks using operator-theoretic techniques. The authors propose a tighter bound than those derived from conventional norm based methods by leveraging small condition numbers in the weight matrices and introducing a tailored Sobolev space as an expanded hypothesis space. This enhanced bound remains valid even in single output settings, outperforming existing Koopman based bounds. The resulting framework maintains key advantages such as flexibility and independence from network width, offering a more precise theoretical understanding of multitask deep learning in the context of kernel methods.

Operator-Based Generalization Bound for Deep Learning: Insights on Multi-Task Learning

This paper presents novel generalization bounds for vector-valued neural networks and deep kernel methods, focusing on multi-task learning through an operator-theoretic framework. Our key development lies in strategically combining a Koopman based approach with existing techniques, achieving tighter generalization guarantees compared to traditional norm-based bounds. To mitigate computational challenges associated with Koopman-based methods, we introduce sketching techniques applicable to vector valued neural networks. These techniques yield excess risk bounds under generic Lipschitz losses, providing performance guarantees for applications including robust and multiple quantile regression. Furthermore, we propose a novel deep learning framework, deep vector-valued reproducing kernel Hilbert spaces (vvRKHS), leveraging Perron Frobenius (PF) operators to enhance deep kernel methods. We derive a new Rademacher generalization bound for this framework, explicitly addressing underfitting and overfitting through kernel refinement strategies. This work offers novel insights into the generalization properties of multitask learning with deep learning architectures, an area that has been relatively unexplored until recent developments.

Gradient Similarity Surgery in Multi-Task Deep Learning

The multi-task learning ($MTL$) paradigm aims to simultaneously learn multiple tasks within a single model capturing higher-level, more general hidden patterns that are shared by the tasks. In deep learning, a significant challenge in the backpropagation training process is the design of advanced optimisers to improve the convergence speed and stability of the gradient descent learning rule. In particular, in multi-task deep learning ($MTDL$) the multitude of tasks may generate potentially conflicting gradients that would hinder the concurrent convergence of the diverse loss functions. This challenge arises when the gradients of the task objectives have either different magnitudes or opposite directions, causing one or a few to dominate or to interfere with each other, thus degrading the training process. Gradient surgery methods address the problem explicitly dealing with conflicting gradients by adjusting the overall gradient trajectory. This work introduces a novel gradient surgery method, the Similarity-Aware Momentum Gradient Surgery (SAM-GS), which provides an effective and scalable approach based on a gradient magnitude similarity measure to guide the optimisation process. The SAM-GS surgery adopts gradient equalisation and modulation of the first-order momentum. A series of experimental tests have shown the effectiveness of SAM-GS on synthetic problems and $MTL$ benchmarks. Gradient magnitude similarity plays a crucial role in regularising gradient aggregation in $MTDL$ for the optimisation of the learning process.

On Learnable Parameters of Optimal and Suboptimal Deep Learning Models

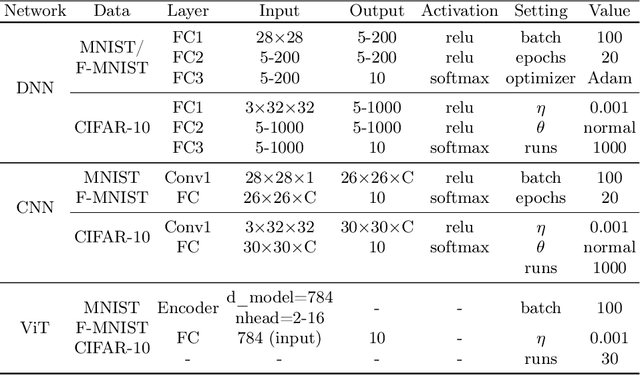
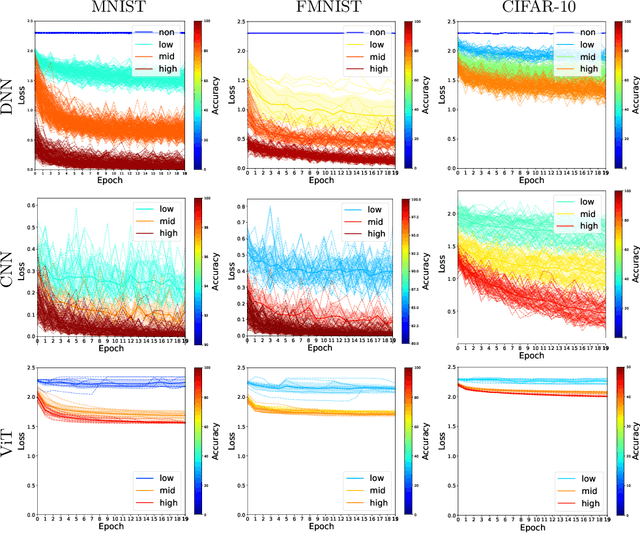
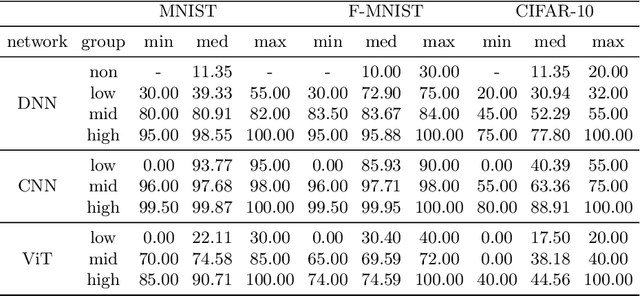
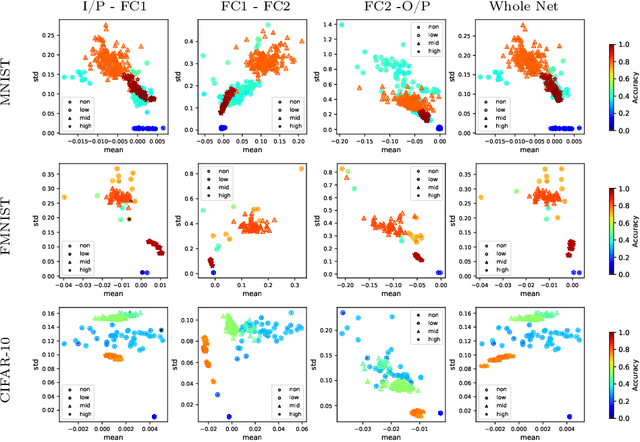
We scrutinize the structural and operational aspects of deep learning models, particularly focusing on the nuances of learnable parameters (weight) statistics, distribution, node interaction, and visualization. By establishing correlations between variance in weight patterns and overall network performance, we investigate the varying (optimal and suboptimal) performances of various deep-learning models. Our empirical analysis extends across widely recognized datasets such as MNIST, Fashion-MNIST, and CIFAR-10, and various deep learning models such as deep neural networks (DNNs), convolutional neural networks (CNNs), and vision transformer (ViT), enabling us to pinpoint characteristics of learnable parameters that correlate with successful networks. Through extensive experiments on the diverse architectures of deep learning models, we shed light on the critical factors that influence the functionality and efficiency of DNNs. Our findings reveal that successful networks, irrespective of datasets or models, are invariably similar to other successful networks in their converged weights statistics and distribution, while poor-performing networks vary in their weights. In addition, our research shows that the learnable parameters of widely varied deep learning models such as DNN, CNN, and ViT exhibit similar learning characteristics.

Deep Neural Networks via Complex Network Theory: a Perspective

Deep Neural Networks (DNNs) can be represented as graphs whose links and vertices iteratively process data and solve tasks sub-optimally. Complex Network Theory (CNT), merging statistical physics with graph theory, provides a method for interpreting neural networks by analysing their weights and neuron structures. However, classic works adapt CNT metrics that only permit a topological analysis as they do not account for the effect of the input data. In addition, CNT metrics have been applied to a limited range of architectures, mainly including Fully Connected neural networks. In this work, we extend the existing CNT metrics with measures that sample from the DNNs' training distribution, shifting from a purely topological analysis to one that connects with the interpretability of deep learning. For the novel metrics, in addition to the existing ones, we provide a mathematical formalisation for Fully Connected, AutoEncoder, Convolutional and Recurrent neural networks, of which we vary the activation functions and the number of hidden layers. We show that these metrics differentiate DNNs based on the architecture, the number of hidden layers, and the activation function. Our contribution provides a method rooted in physics for interpreting DNNs that offers insights beyond the traditional input-output relationship and the CNT topological analysis.

Fragility, Robustness and Antifragility in Deep Learning

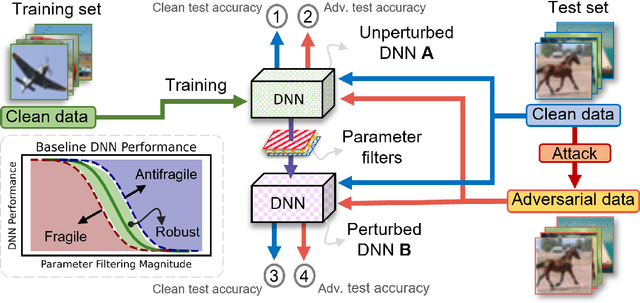
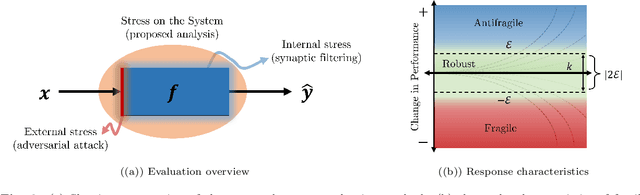
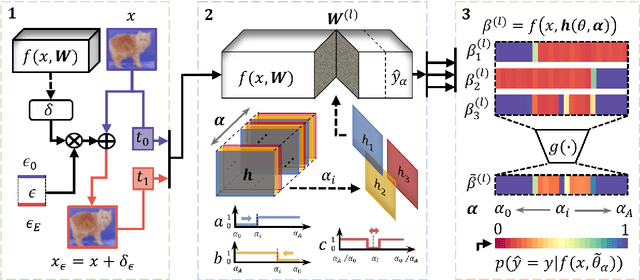
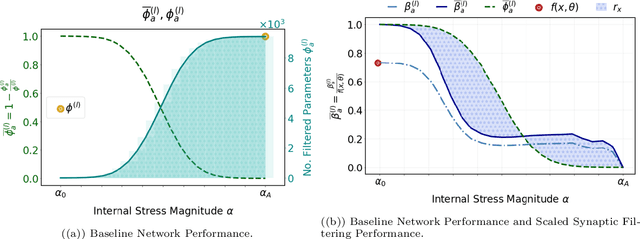
We propose a systematic analysis of deep neural networks (DNNs) based on a signal processing technique for network parameter removal, in the form of synaptic filters that identifies the fragility, robustness and antifragility characteristics of DNN parameters. Our proposed analysis investigates if the DNN performance is impacted negatively, invariantly, or positively on both clean and adversarially perturbed test datasets when the DNN undergoes synaptic filtering. We define three \textit{filtering scores} for quantifying the fragility, robustness and antifragility characteristics of DNN parameters based on the performances for (i) clean dataset, (ii) adversarial dataset, and (iii) the difference in performances of clean and adversarial datasets. We validate the proposed systematic analysis on ResNet-18, ResNet-50, SqueezeNet-v1.1 and ShuffleNet V2 x1.0 network architectures for MNIST, CIFAR10 and Tiny ImageNet datasets. The filtering scores, for a given network architecture, identify network parameters that are invariant in characteristics across different datasets over learning epochs. Vice-versa, for a given dataset, the filtering scores identify the parameters that are invariant in characteristics across different network architectures. We show that our synaptic filtering method improves the test accuracy of ResNet and ShuffleNet models on adversarial datasets when only the robust and antifragile parameters are selectively retrained at any given epoch, thus demonstrating applications of the proposed strategy in improving model robustness.

Adaptive search space decomposition method for pre- and post- buckling analyses of space truss structures

The paper proposes a novel adaptive search space decomposition method and a novel gradient-free optimization-based formulation for the pre- and post-buckling analyses of space truss structures. Space trusses are often employed in structural engineering to build large steel constructions, such as bridges and domes, whose structural response is characterized by large displacements. Therefore, these structures are vulnerable to progressive collapses due to local or global buckling effects, leading to sudden failures. The method proposed in this paper allows the analysis of the load-equilibrium path of truss structures to permanent and variable loading, including stable and unstable equilibrium stages and explicitly considering geometric nonlinearities. The goal of this work is to determine these equilibrium stages via optimization of the Lagrangian kinematic parameters of the system, determining the global equilibrium. However, this optimization problem is non-trivial due to the undefined parameter domain and the sensitivity and interaction among the Lagrangian parameters. Therefore, we propose formulating this problem as a nonlinear, multimodal, unconstrained, continuous optimization problem and develop a novel adaptive search space decomposition method, which progressively and adaptively re-defines the search domain (hypersphere) to evaluate the equilibrium of the system using a gradient-free optimization algorithm. We tackle three benchmark problems and evaluate a medium-sized test representing a real structural problem in this paper. The results are compared to those available in the literature regarding displacement-load curves and deformed configurations. The accuracy and robustness of the adopted methodology show a high potential of gradient-free algorithms in analyzing space truss structures.

Deep Neural Networks as Complex Networks

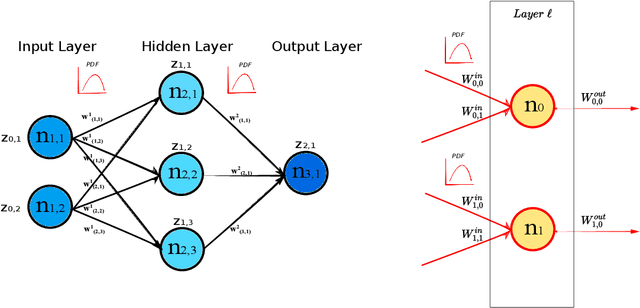
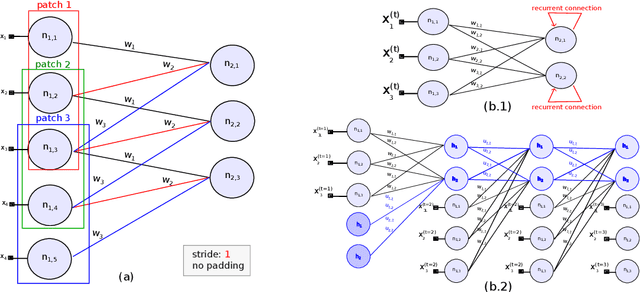
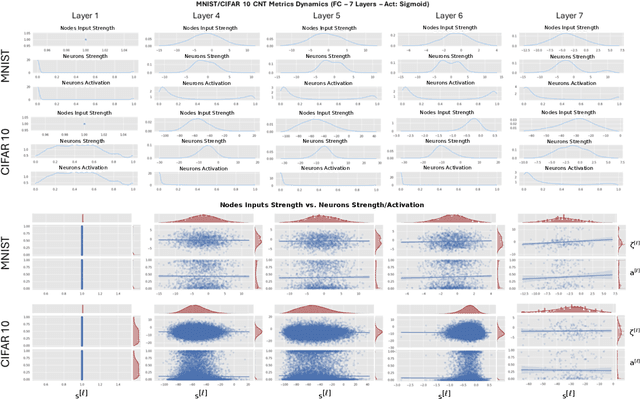
Deep Neural Networks are, from a physical perspective, graphs whose `links` and `vertices` iteratively process data and solve tasks sub-optimally. We use Complex Network Theory (CNT) to represents Deep Neural Networks (DNNs) as directed weighted graphs: within this framework, we introduce metrics to study DNNs as dynamical systems, with a granularity that spans from weights to layers, including neurons. CNT discriminates networks that differ in the number of parameters and neurons, the type of hidden layers and activations, and the objective task. We further show that our metrics discriminate low vs. high performing networks. CNT is a comprehensive method to reason about DNNs and a complementary approach to explain a model's behavior that is physically grounded to networks theory and goes beyond the well-studied input-output relation.

Assessing Ranking and Effectiveness of Evolutionary Algorithm Hyperparameters Using Global Sensitivity Analysis Methodologies

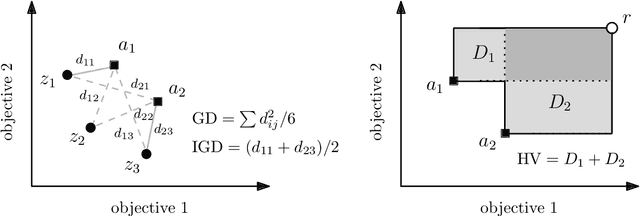
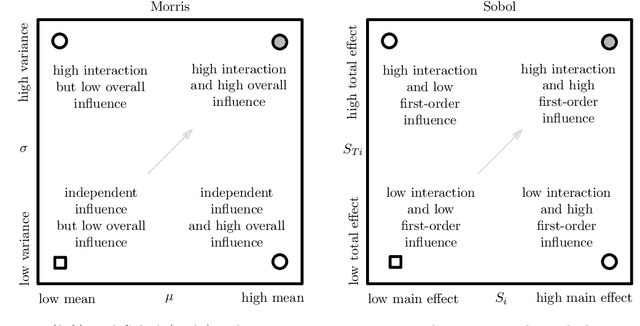
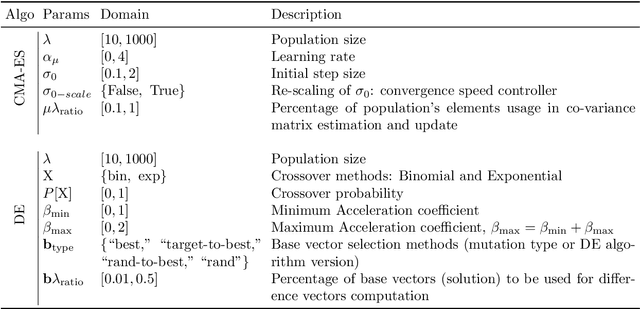
We present a comprehensive global sensitivity analysis of two single-objective and two multi-objective state-of-the-art global optimization evolutionary algorithms as an algorithm configuration problem. That is, we investigate the quality of influence hyperparameters have on the performance of algorithms in terms of their direct effect and interaction effect with other hyperparameters. Using three sensitivity analysis methods, Morris LHS, Morris, and Sobol, to systematically analyze tunable hyperparameters of covariance matrix adaptation evolutionary strategy, differential evolution, non-dominated sorting genetic algorithm III, and multi-objective evolutionary algorithm based on decomposition, the framework reveals the behaviors of hyperparameters to sampling methods and performance metrics. That is, it answers questions like what hyperparameters influence patterns, how they interact, how much they interact, and how much their direct influence is. Consequently, the ranking of hyperparameters suggests their order of tuning, and the pattern of influence reveals the stability of the algorithms.

Backpropagation Neural Tree

We propose a novel algorithm called Backpropagation Neural Tree (BNeuralT), which is a stochastic computational dendritic tree. BNeuralT takes random repeated inputs through its leaves and imposes dendritic nonlinearities through its internal connections like a biological dendritic tree would do. Considering the dendritic-tree like plausible biological properties, BNeuralT is a single neuron neural tree model with its internal sub-trees resembling dendritic nonlinearities. BNeuralT algorithm produces an ad hoc neural tree which is trained using a stochastic gradient descent optimizer like gradient descent (GD), momentum GD, Nesterov accelerated GD, Adagrad, RMSprop, or Adam. BNeuralT training has two phases, each computed in a depth-first search manner: the forward pass computes neural tree's output in a post-order traversal, while the error backpropagation during the backward pass is performed recursively in a pre-order traversal. A BNeuralT model can be considered a minimal subset of a neural network (NN), meaning it is a "thinned" NN whose complexity is lower than an ordinary NN. Our algorithm produces high-performing and parsimonious models balancing the complexity with descriptive ability on a wide variety of machine learning problems: classification, regression, and pattern recognition.