Gabriele La Malfa
Fairness Aware Reinforcement Learning via Proximal Policy Optimization
Feb 06, 2025Abstract:Fairness in multi-agent systems (MAS) focuses on equitable reward distribution among agents in scenarios involving sensitive attributes such as race, gender, or socioeconomic status. This paper introduces fairness in Proximal Policy Optimization (PPO) with a penalty term derived from demographic parity, counterfactual fairness, and conditional statistical parity. The proposed method balances reward maximisation with fairness by integrating two penalty components: a retrospective component that minimises disparities in past outcomes and a prospective component that ensures fairness in future decision-making. We evaluate our approach in the Allelopathic Harvest game, a cooperative and competitive MAS focused on resource collection, where some agents possess a sensitive attribute. Experiments demonstrate that fair-PPO achieves fairer policies across all fairness metrics than classic PPO. Fairness comes at the cost of reduced rewards, namely the Price of Fairness, although agents with and without the sensitive attribute renounce comparable amounts of rewards. Additionally, the retrospective and prospective penalties effectively change the agents' behaviour and improve fairness. These findings underscore the potential of fair-PPO to address fairness challenges in MAS.
Using Protected Attributes to Consider Fairness in Multi-Agent Systems
Oct 16, 2024Abstract:Fairness in Multi-Agent Systems (MAS) has been extensively studied, particularly in reward distribution among agents in scenarios such as goods allocation, resource division, lotteries, and bargaining systems. Fairness in MAS depends on various factors, including the system's governing rules, the behaviour of the agents, and their characteristics. Yet, fairness in human society often involves evaluating disparities between disadvantaged and privileged groups, guided by principles of Equality, Diversity, and Inclusion (EDI). Taking inspiration from the work on algorithmic fairness, which addresses bias in machine learning-based decision-making, we define protected attributes for MAS as characteristics that should not disadvantage an agent in terms of its expected rewards. We adapt fairness metrics from the algorithmic fairness literature -- namely, demographic parity, counterfactual fairness, and conditional statistical parity -- to the multi-agent setting, where self-interested agents interact within an environment. These metrics allow us to evaluate the fairness of MAS, with the ultimate aim of designing MAS that do not disadvantage agents based on protected attributes.
Deep Neural Networks via Complex Network Theory: a Perspective
Apr 18, 2024Abstract:Deep Neural Networks (DNNs) can be represented as graphs whose links and vertices iteratively process data and solve tasks sub-optimally. Complex Network Theory (CNT), merging statistical physics with graph theory, provides a method for interpreting neural networks by analysing their weights and neuron structures. However, classic works adapt CNT metrics that only permit a topological analysis as they do not account for the effect of the input data. In addition, CNT metrics have been applied to a limited range of architectures, mainly including Fully Connected neural networks. In this work, we extend the existing CNT metrics with measures that sample from the DNNs' training distribution, shifting from a purely topological analysis to one that connects with the interpretability of deep learning. For the novel metrics, in addition to the existing ones, we provide a mathematical formalisation for Fully Connected, AutoEncoder, Convolutional and Recurrent neural networks, of which we vary the activation functions and the number of hidden layers. We show that these metrics differentiate DNNs based on the architecture, the number of hidden layers, and the activation function. Our contribution provides a method rooted in physics for interpreting DNNs that offers insights beyond the traditional input-output relationship and the CNT topological analysis.
Deep Neural Networks as Complex Networks
Sep 12, 2022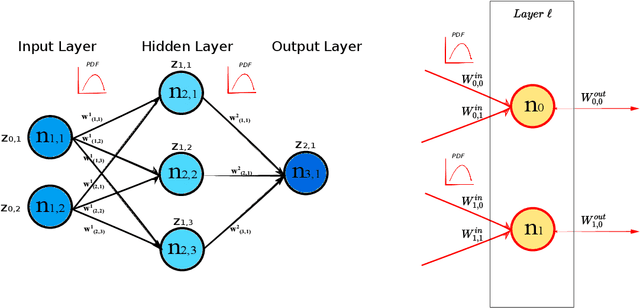

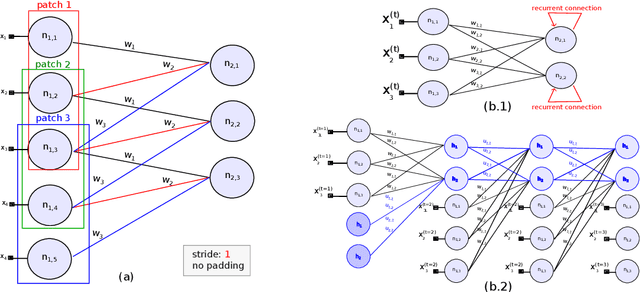
Abstract:Deep Neural Networks are, from a physical perspective, graphs whose `links` and `vertices` iteratively process data and solve tasks sub-optimally. We use Complex Network Theory (CNT) to represents Deep Neural Networks (DNNs) as directed weighted graphs: within this framework, we introduce metrics to study DNNs as dynamical systems, with a granularity that spans from weights to layers, including neurons. CNT discriminates networks that differ in the number of parameters and neurons, the type of hidden layers and activations, and the objective task. We further show that our metrics discriminate low vs. high performing networks. CNT is a comprehensive method to reason about DNNs and a complementary approach to explain a model's behavior that is physically grounded to networks theory and goes beyond the well-studied input-output relation.
Characterizing Learning Dynamics of Deep Neural Networks via Complex Networks
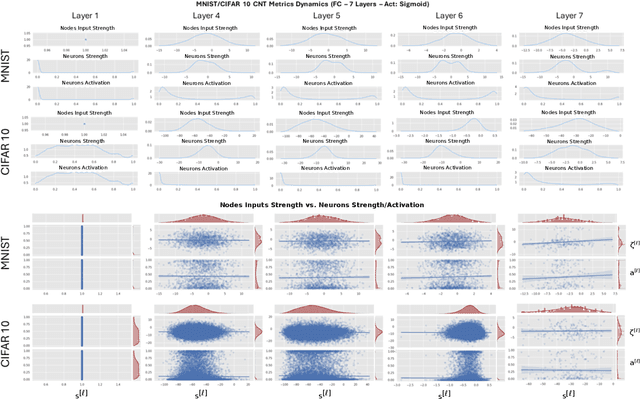
Oct 18, 2021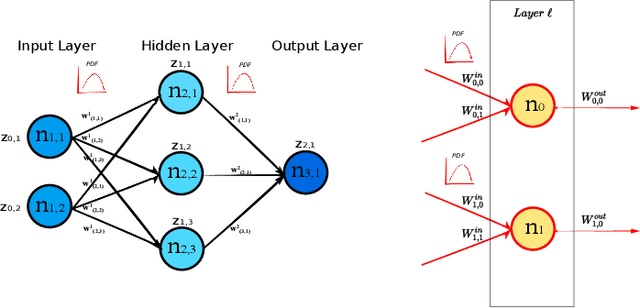
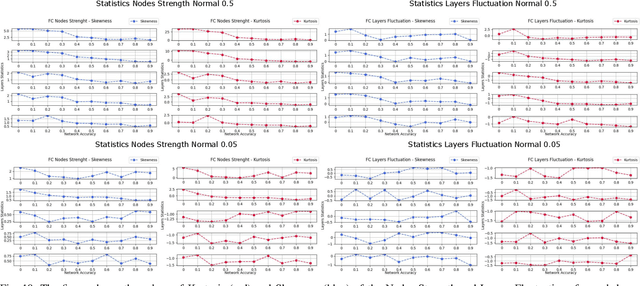
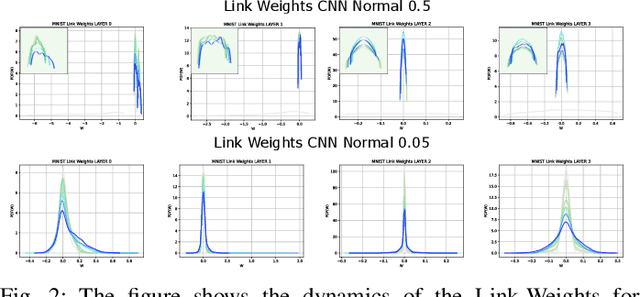
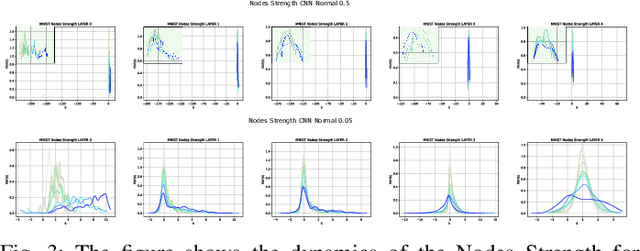
Abstract:In this paper, we interpret Deep Neural Networks with Complex Network Theory. Complex Network Theory (CNT) represents Deep Neural Networks (DNNs) as directed weighted graphs to study them as dynamical systems. We efficiently adapt CNT measures to examine the evolution of the learning process of DNNs with different initializations and architectures: we introduce metrics for nodes/neurons and layers, namely Nodes Strength and Layers Fluctuation. Our framework distills trends in the learning dynamics and separates low from high accurate networks. We characterize populations of neural networks (ensemble analysis) and single instances (individual analysis). We tackle standard problems of image recognition, for which we show that specific learning dynamics are indistinguishable when analysed through the solely Link-Weights analysis. Further, Nodes Strength and Layers Fluctuations make unprecedented behaviours emerge: accurate networks, when compared to under-trained models, show substantially divergent distributions with the greater extremity of deviations. On top of this study, we provide an efficient implementation of the CNT metrics for both Convolutional and Fully Connected Networks, to fasten the research in this direction.
* IEEE/ICTAI2021 (full paper)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge