On Learnable Parameters of Optimal and Suboptimal Deep Learning Models

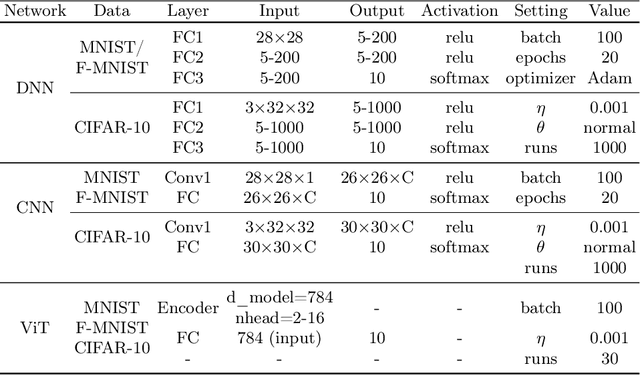
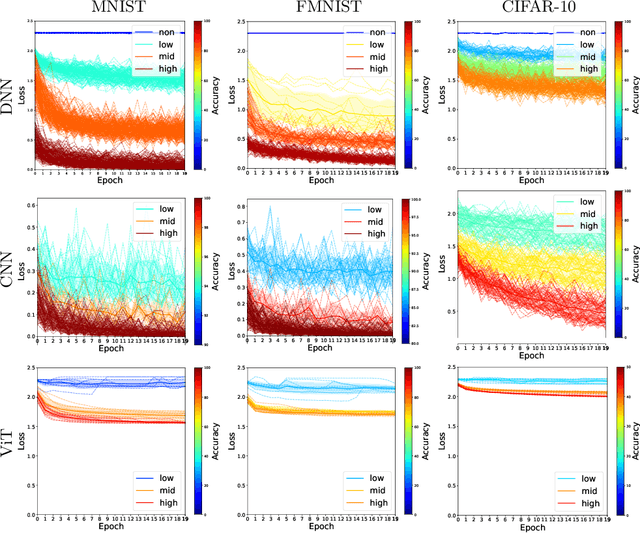
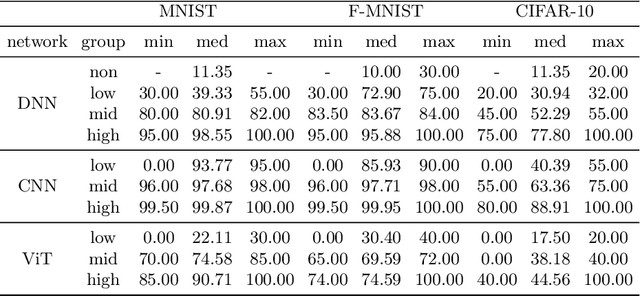
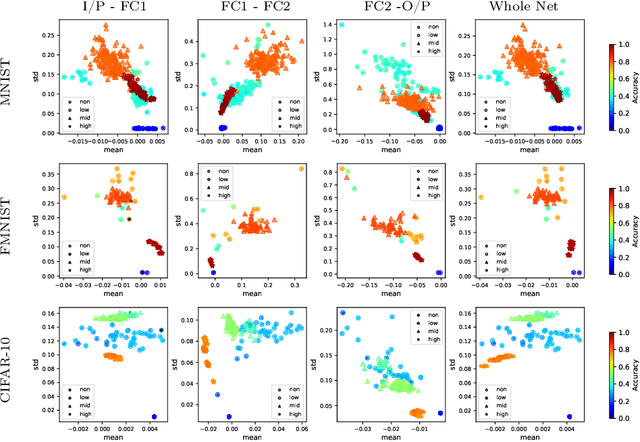
We scrutinize the structural and operational aspects of deep learning models, particularly focusing on the nuances of learnable parameters (weight) statistics, distribution, node interaction, and visualization. By establishing correlations between variance in weight patterns and overall network performance, we investigate the varying (optimal and suboptimal) performances of various deep-learning models. Our empirical analysis extends across widely recognized datasets such as MNIST, Fashion-MNIST, and CIFAR-10, and various deep learning models such as deep neural networks (DNNs), convolutional neural networks (CNNs), and vision transformer (ViT), enabling us to pinpoint characteristics of learnable parameters that correlate with successful networks. Through extensive experiments on the diverse architectures of deep learning models, we shed light on the critical factors that influence the functionality and efficiency of DNNs. Our findings reveal that successful networks, irrespective of datasets or models, are invariably similar to other successful networks in their converged weights statistics and distribution, while poor-performing networks vary in their weights. In addition, our research shows that the learnable parameters of widely varied deep learning models such as DNN, CNN, and ViT exhibit similar learning characteristics.

Deep Neural Networks via Complex Network Theory: a Perspective

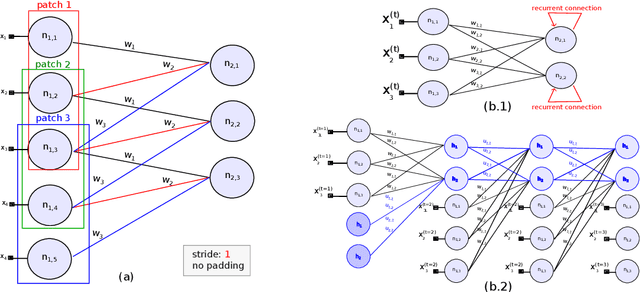
Deep Neural Networks (DNNs) can be represented as graphs whose links and vertices iteratively process data and solve tasks sub-optimally. Complex Network Theory (CNT), merging statistical physics with graph theory, provides a method for interpreting neural networks by analysing their weights and neuron structures. However, classic works adapt CNT metrics that only permit a topological analysis as they do not account for the effect of the input data. In addition, CNT metrics have been applied to a limited range of architectures, mainly including Fully Connected neural networks. In this work, we extend the existing CNT metrics with measures that sample from the DNNs' training distribution, shifting from a purely topological analysis to one that connects with the interpretability of deep learning. For the novel metrics, in addition to the existing ones, we provide a mathematical formalisation for Fully Connected, AutoEncoder, Convolutional and Recurrent neural networks, of which we vary the activation functions and the number of hidden layers. We show that these metrics differentiate DNNs based on the architecture, the number of hidden layers, and the activation function. Our contribution provides a method rooted in physics for interpreting DNNs that offers insights beyond the traditional input-output relationship and the CNT topological analysis.

Deep Neural Networks as Complex Networks

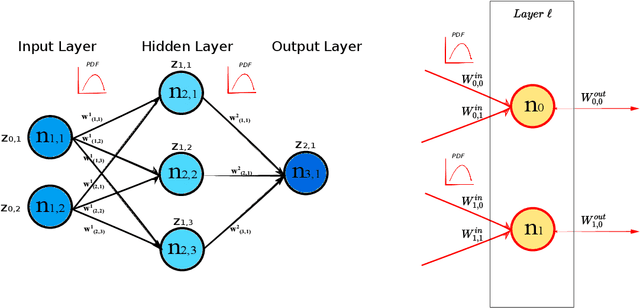
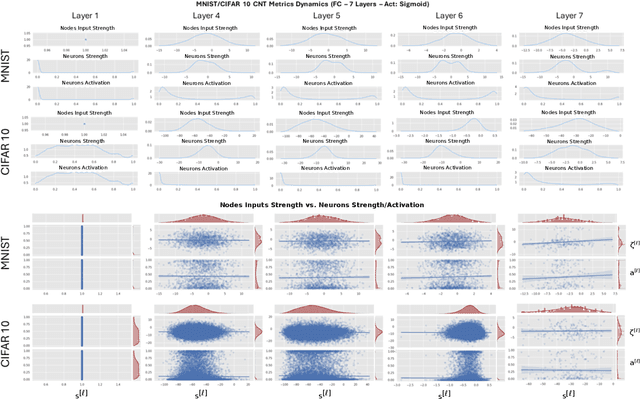
Deep Neural Networks are, from a physical perspective, graphs whose `links` and `vertices` iteratively process data and solve tasks sub-optimally. We use Complex Network Theory (CNT) to represents Deep Neural Networks (DNNs) as directed weighted graphs: within this framework, we introduce metrics to study DNNs as dynamical systems, with a granularity that spans from weights to layers, including neurons. CNT discriminates networks that differ in the number of parameters and neurons, the type of hidden layers and activations, and the objective task. We further show that our metrics discriminate low vs. high performing networks. CNT is a comprehensive method to reason about DNNs and a complementary approach to explain a model's behavior that is physically grounded to networks theory and goes beyond the well-studied input-output relation.

MultiSAGE: a multiplex embedding algorithm for inter-layer link prediction

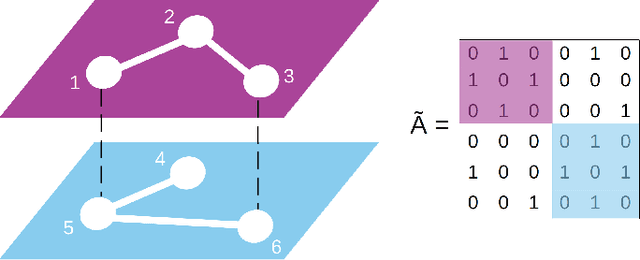
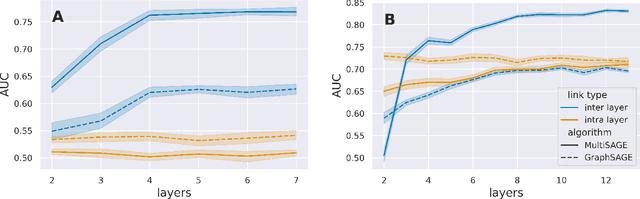
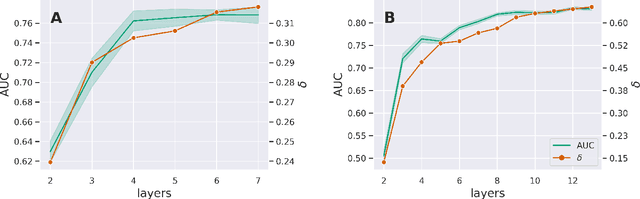
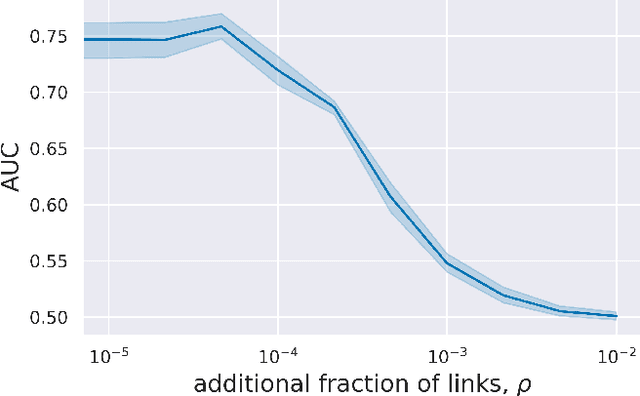
Research on graph representation learning has received great attention in recent years. However, most of the studies so far have focused on the embedding of single-layer graphs. The few studies dealing with the problem of representation learning of multilayer structures rely on the strong hypothesis that the inter-layer links are known, and this limits the range of possible applications. Here we propose MultiSAGE, a generalization of the GraphSAGE algorithm that allows to embed multiplex networks. We show that MultiSAGE is capable to reconstruct both the intra-layer and the inter-layer connectivity, outperforming GraphSAGE, which has been designed for simple graphs. Next, through a comprehensive experimental analysis, we shed light also on the performance of the embedding, both in simple and in multiplex networks, showing that either the density of the graph or the randomness of the links strongly influences the quality of the embedding.

Characterizing Learning Dynamics of Deep Neural Networks via Complex Networks

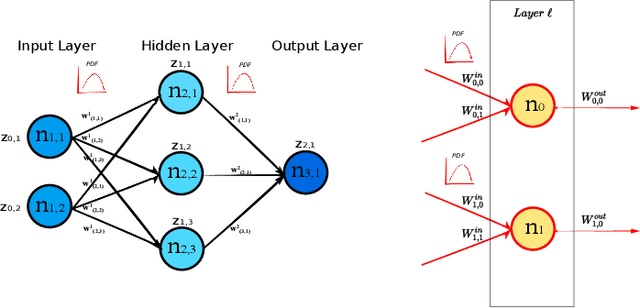
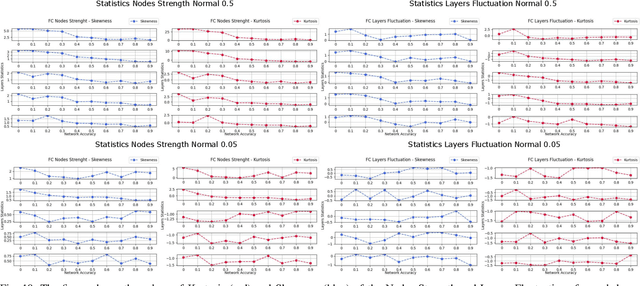
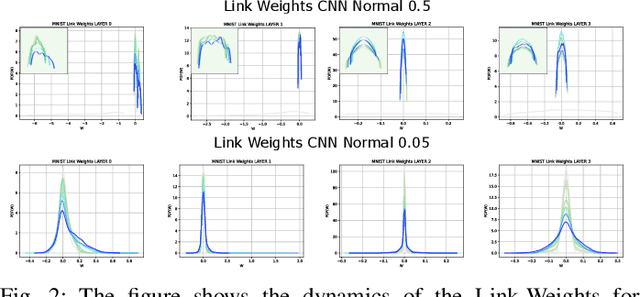
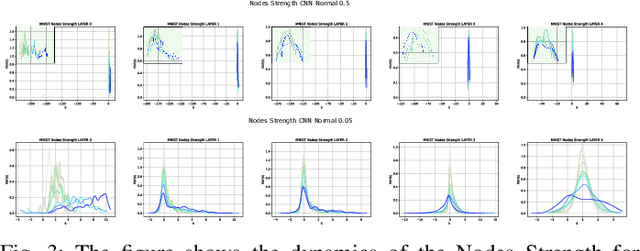
In this paper, we interpret Deep Neural Networks with Complex Network Theory. Complex Network Theory (CNT) represents Deep Neural Networks (DNNs) as directed weighted graphs to study them as dynamical systems. We efficiently adapt CNT measures to examine the evolution of the learning process of DNNs with different initializations and architectures: we introduce metrics for nodes/neurons and layers, namely Nodes Strength and Layers Fluctuation. Our framework distills trends in the learning dynamics and separates low from high accurate networks. We characterize populations of neural networks (ensemble analysis) and single instances (individual analysis). We tackle standard problems of image recognition, for which we show that specific learning dynamics are indistinguishable when analysed through the solely Link-Weights analysis. Further, Nodes Strength and Layers Fluctuations make unprecedented behaviours emerge: accurate networks, when compared to under-trained models, show substantially divergent distributions with the greater extremity of deviations. On top of this study, we provide an efficient implementation of the CNT metrics for both Convolutional and Fully Connected Networks, to fasten the research in this direction.