Converting Transformers to Polynomial Form for Secure Inference Over Homomorphic Encryption

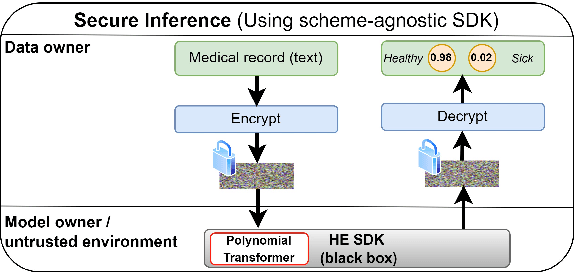
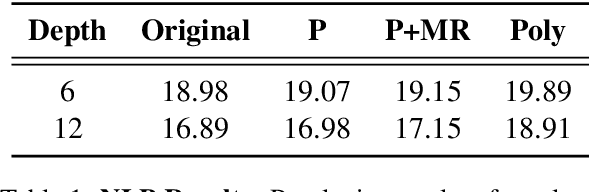
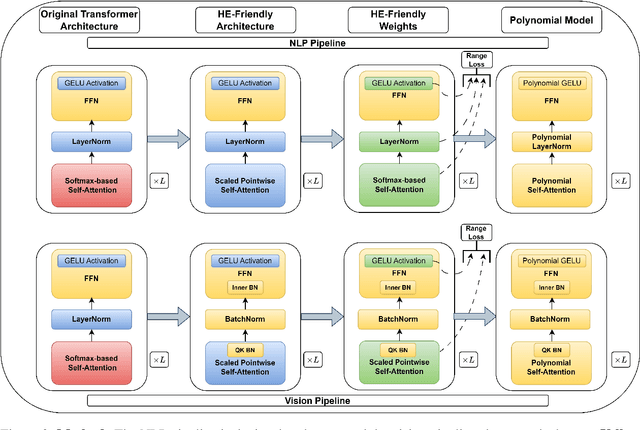
Designing privacy-preserving deep learning models is a major challenge within the deep learning community. Homomorphic Encryption (HE) has emerged as one of the most promising approaches in this realm, enabling the decoupling of knowledge between the model owner and the data owner. Despite extensive research and application of this technology, primarily in convolutional neural networks, incorporating HE into transformer models has been challenging because of the difficulties in converting these models into a polynomial form. We break new ground by introducing the first polynomial transformer, providing the first demonstration of secure inference over HE with transformers. This includes a transformer architecture tailored for HE, alongside a novel method for converting operators to their polynomial equivalent. This innovation enables us to perform secure inference on LMs with WikiText-103. It also allows us to perform image classification with CIFAR-100 and Tiny-ImageNet. Our models yield results comparable to traditional methods, bridging the performance gap with transformers of similar scale and underscoring the viability of HE for state-of-the-art applications. Finally, we assess the stability of our models and conduct a series of ablations to quantify the contribution of each model component.

Sensitive Tuning of Large Scale CNNs for E2E Secure Prediction using Homomorphic Encryption

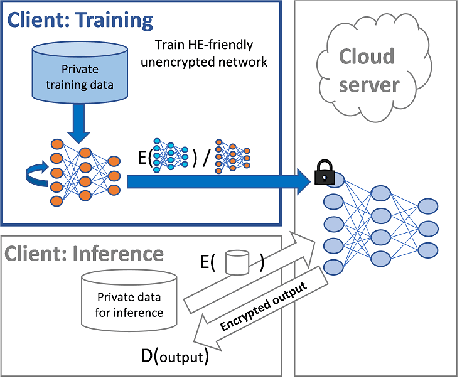
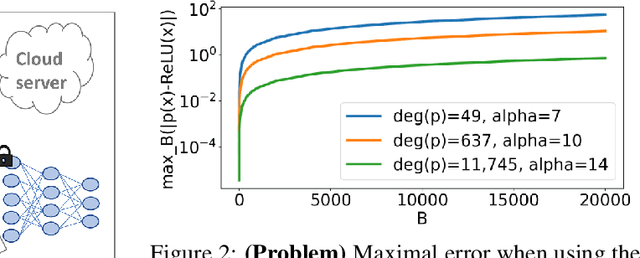
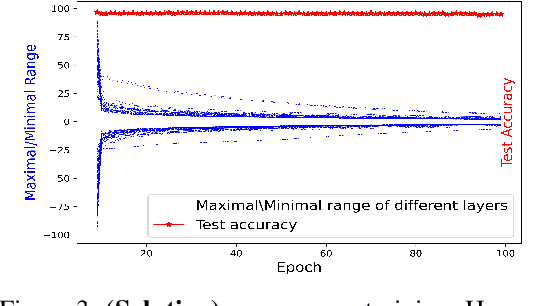
Privacy-preserving machine learning solutions have recently gained significant attention. One promising research trend is using Homomorphic Encryption (HE), a method for performing computation over encrypted data. One major challenge in this approach is training HE-friendly, encrypted or unencrypted, deep CNNs with decent accuracy. We propose a novel training method for HE-friendly models, and demonstrate it on fundamental and modern CNNs, such as ResNet and ConvNeXt. After training, we evaluate our models by running encrypted samples using HELayers SDK and proving that they yield the desired results. When running on a GPU over the ImageNet dataset, our ResNet-18/50/101 implementations take only 7, 31 and 57 minutes, respectively, which shows that this solution is practical. Furthermore, we present several insights on handling the activation functions and skip-connections under HE. Finally, we demonstrate in an unprecedented way how to perform secure zero-shot prediction using a CLIP model that we adapted to be HE-friendly.

Tile Tensors: A versatile data structure with descriptive shapes for homomorphic encryption

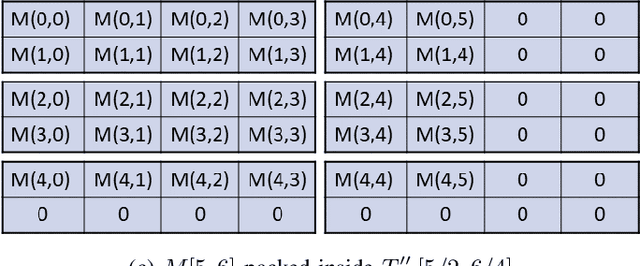
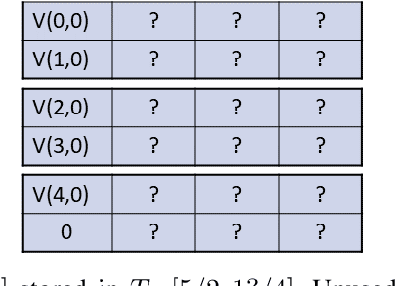
Moving from the theoretical promise of Fully Homomorphic Encryption (FHE) to real-world applications with realistic and acceptable time and memory figures is an on-going challenge. After choosing an appropriate FHE scheme, and before implementing privacy-preserving analytics, one needs an efficient packing method that will optimize use of the ciphertext slots, trading-off size, latency, and throughput. We propose a solution to this challenge. We describe a method for efficiently working with tensors (multi-dimensional arrays) in a system that imposes tiles, i.e., fixed-size vectors. The tensors are packed into tiles and then manipulated via operations on those tiles. We further show a novel and concise notation for describing packing details. Our method reinterprets the tiles as multi-dimensional arrays, and combines them to cover enough space to hold the tensor. An efficient summation algorithm can then sum over any dimension of this construct. We propose a descriptive notation for the shape of this data structure that describes both the original tensor and how it is packed inside the tiles. Our solution can be used to optimize the performance of various algorithms such as consecutive matrix multiplications or neural network inference with varying batch sizes. It can also serve to enhance optimizations done by homomorphic encryption compilers. We describe different applications that take advantage of this data structure through the proposed notation, experiment to evaluate the advantages through different applications, and share our conclusions.

Data Minimization for GDPR Compliance in Machine Learning Models

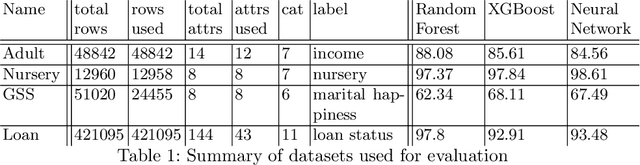
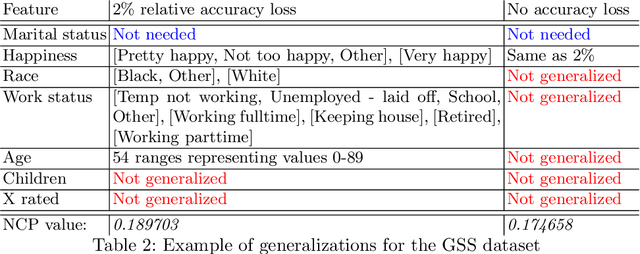
The EU General Data Protection Regulation (GDPR) mandates the principle of data minimization, which requires that only data necessary to fulfill a certain purpose be collected. However, it can often be difficult to determine the minimal amount of data required, especially in complex machine learning models such as neural networks. We present a first-of-a-kind method to reduce the amount of personal data needed to perform predictions with a machine learning model, by removing or generalizing some of the input features. Our method makes use of the knowledge encoded within the model to produce a generalization that has little to no impact on its accuracy. This enables the creators and users of machine learning models to acheive data minimization, in a provable manner.

Anonymizing Machine Learning Models

There is a known tension between the need to analyze personal data to drive business and privacy concerns. Many data protection regulations, including the EU General Data Protection Regulation (GDPR) and the California Consumer Protection Act (CCPA), set out strict restrictions and obligations on companies that collect or process personal data. Moreover, machine learning models themselves can be used to derive personal information, as demonstrated by recent membership and attribute inference attacks. Anonymized data, however, is exempt from data protection principles and obligations. Thus, models built on anonymized data are also exempt from any privacy obligations, in addition to providing better protection against such attacks on the training data. Learning on anonymized data typically results in a significant degradation in accuracy. We address this challenge by guiding our anonymization using the knowledge encoded within the model, and targeting it to minimize the impact on the model's accuracy, a process we call accuracy-guided anonymization. We demonstrate that by focusing on the model's accuracy rather than information loss, our method outperforms state of the art k-anonymity methods in terms of the achieved utility, in particular with high values of k and large numbers of quasi-identifiers. We also demonstrate that our approach achieves similar results in its ability to prevent membership inference attacks as alternative approaches based on differential privacy. This shows that model-guided anonymization can, in some cases, be a legitimate substitute for such methods, while averting some of their inherent drawbacks such as complexity, performance overhead and being fitted to specific model types. As opposed to methods that rely on adding noise during training, our approach does not rely on making any modifications to the training algorithm itself.

Reducing Risk of Model Inversion Using Privacy-Guided Training

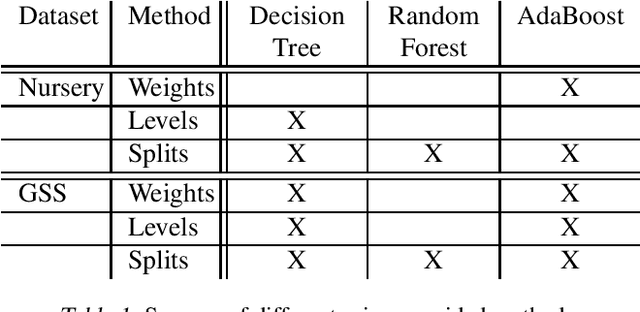
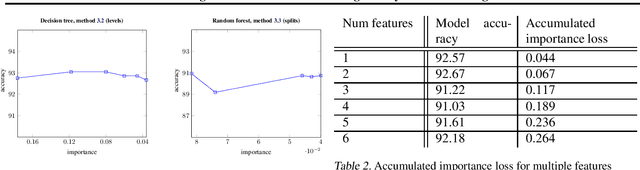
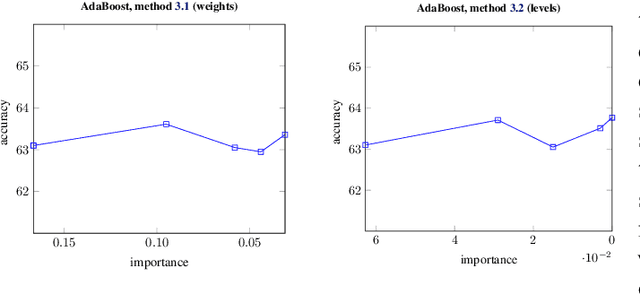
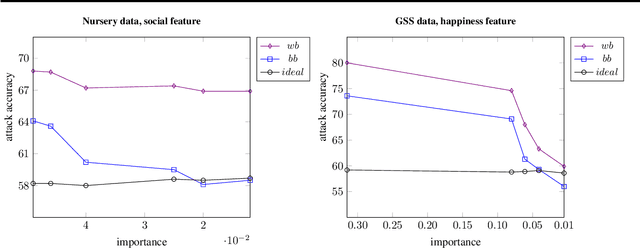
Machine learning models often pose a threat to the privacy of individuals whose data is part of the training set. Several recent attacks have been able to infer sensitive information from trained models, including model inversion or attribute inference attacks. These attacks are able to reveal the values of certain sensitive features of individuals who participated in training the model. It has also been shown that several factors can contribute to an increased risk of model inversion, including feature influence. We observe that not all features necessarily share the same level of privacy or sensitivity. In many cases, certain features used to train a model are considered especially sensitive and therefore propitious candidates for inversion. We present a solution for countering model inversion attacks in tree-based models, by reducing the influence of sensitive features in these models. This is an avenue that has not yet been thoroughly investigated, with only very nascent previous attempts at using this as a countermeasure against attribute inference. Our work shows that, in many cases, it is possible to train a model in different ways, resulting in different influence levels of the various features, without necessarily harming the model's accuracy. We are able to utilize this fact to train models in a manner that reduces the model's reliance on the most sensitive features, while increasing the importance of less sensitive features. Our evaluation confirms that training models in this manner reduces the risk of inference for those features, as demonstrated through several black-box and white-box attacks.