Power-Softmax: Towards Secure LLM Inference over Encrypted Data

Modern cryptographic methods for implementing privacy-preserving LLMs such as Homomorphic Encryption (HE) require the LLMs to have a polynomial form. Forming such a representation is challenging because Transformers include non-polynomial components, such as Softmax and layer normalization. Previous approaches have either directly approximated pre-trained models with large-degree polynomials, which are less efficient over HE, or replaced non-polynomial components with easier-to-approximate primitives before training, e.g., Softmax with pointwise attention. The latter approach might introduce scalability challenges. We present a new HE-friendly variant of self-attention that offers a stable form for training and is easy to approximate with polynomials for secure inference. Our work introduces the first polynomial LLMs with 32 layers and over a billion parameters, exceeding the size of previous models by more than tenfold. The resulting models demonstrate reasoning and in-context learning (ICL) capabilities comparable to standard transformers of the same size, representing a breakthrough in the field. Finally, we provide a detailed latency breakdown for each computation over encrypted data, paving the way for further optimization, and explore the differences in inductive bias between transformers relying on our HE-friendly variant and standard transformers. Our code is attached as a supplement.

Sensitive Tuning of Large Scale CNNs for E2E Secure Prediction using Homomorphic Encryption

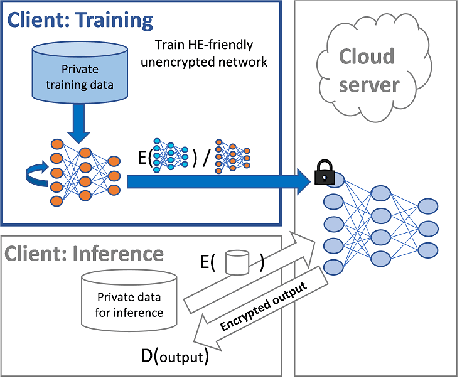
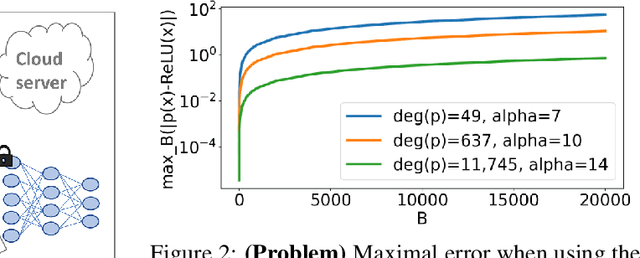
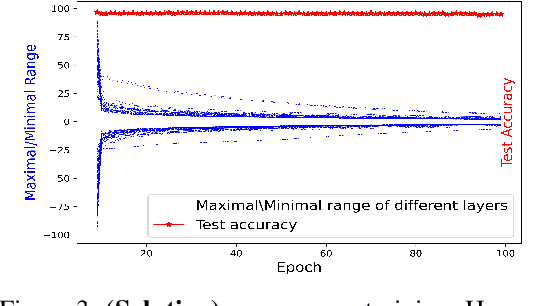
Privacy-preserving machine learning solutions have recently gained significant attention. One promising research trend is using Homomorphic Encryption (HE), a method for performing computation over encrypted data. One major challenge in this approach is training HE-friendly, encrypted or unencrypted, deep CNNs with decent accuracy. We propose a novel training method for HE-friendly models, and demonstrate it on fundamental and modern CNNs, such as ResNet and ConvNeXt. After training, we evaluate our models by running encrypted samples using HELayers SDK and proving that they yield the desired results. When running on a GPU over the ImageNet dataset, our ResNet-18/50/101 implementations take only 7, 31 and 57 minutes, respectively, which shows that this solution is practical. Furthermore, we present several insights on handling the activation functions and skip-connections under HE. Finally, we demonstrate in an unprecedented way how to perform secure zero-shot prediction using a CLIP model that we adapted to be HE-friendly.