Power-Softmax: Towards Secure LLM Inference over Encrypted Data

Modern cryptographic methods for implementing privacy-preserving LLMs such as Homomorphic Encryption (HE) require the LLMs to have a polynomial form. Forming such a representation is challenging because Transformers include non-polynomial components, such as Softmax and layer normalization. Previous approaches have either directly approximated pre-trained models with large-degree polynomials, which are less efficient over HE, or replaced non-polynomial components with easier-to-approximate primitives before training, e.g., Softmax with pointwise attention. The latter approach might introduce scalability challenges. We present a new HE-friendly variant of self-attention that offers a stable form for training and is easy to approximate with polynomials for secure inference. Our work introduces the first polynomial LLMs with 32 layers and over a billion parameters, exceeding the size of previous models by more than tenfold. The resulting models demonstrate reasoning and in-context learning (ICL) capabilities comparable to standard transformers of the same size, representing a breakthrough in the field. Finally, we provide a detailed latency breakdown for each computation over encrypted data, paving the way for further optimization, and explore the differences in inductive bias between transformers relying on our HE-friendly variant and standard transformers. Our code is attached as a supplement.

Tile Tensors: A versatile data structure with descriptive shapes for homomorphic encryption

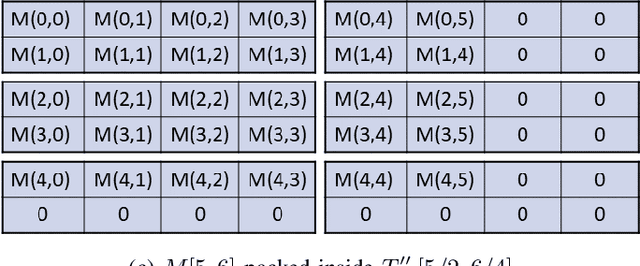
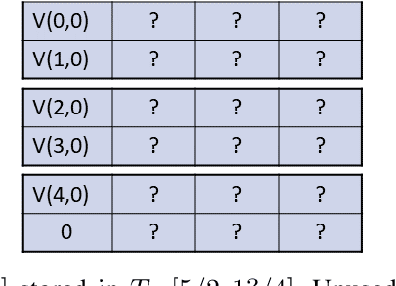
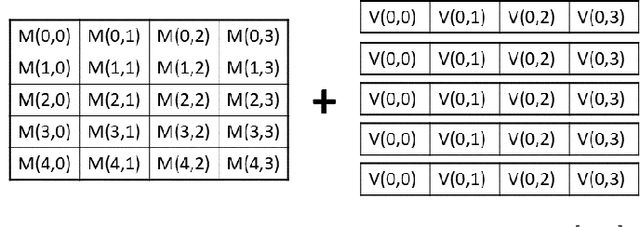
Moving from the theoretical promise of Fully Homomorphic Encryption (FHE) to real-world applications with realistic and acceptable time and memory figures is an on-going challenge. After choosing an appropriate FHE scheme, and before implementing privacy-preserving analytics, one needs an efficient packing method that will optimize use of the ciphertext slots, trading-off size, latency, and throughput. We propose a solution to this challenge. We describe a method for efficiently working with tensors (multi-dimensional arrays) in a system that imposes tiles, i.e., fixed-size vectors. The tensors are packed into tiles and then manipulated via operations on those tiles. We further show a novel and concise notation for describing packing details. Our method reinterprets the tiles as multi-dimensional arrays, and combines them to cover enough space to hold the tensor. An efficient summation algorithm can then sum over any dimension of this construct. We propose a descriptive notation for the shape of this data structure that describes both the original tensor and how it is packed inside the tiles. Our solution can be used to optimize the performance of various algorithms such as consecutive matrix multiplications or neural network inference with varying batch sizes. It can also serve to enhance optimizations done by homomorphic encryption compilers. We describe different applications that take advantage of this data structure through the proposed notation, experiment to evaluate the advantages through different applications, and share our conclusions.