SLIP: Securing LLMs IP Using Weights Decomposition

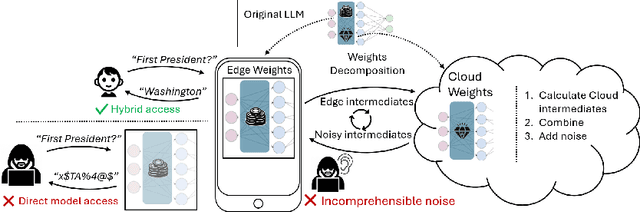
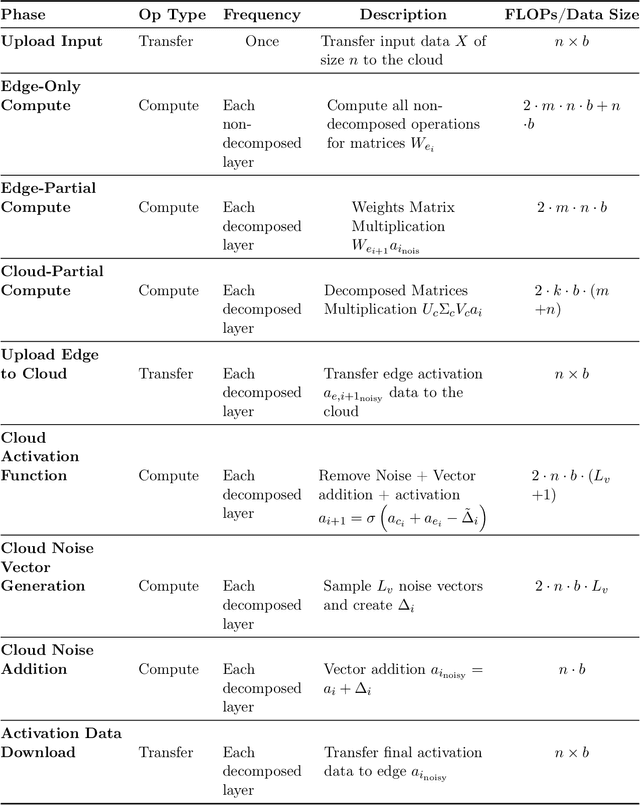
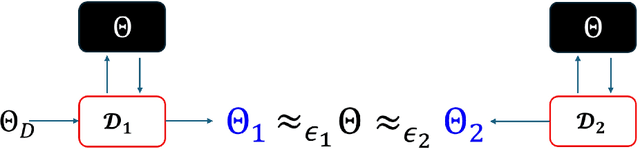
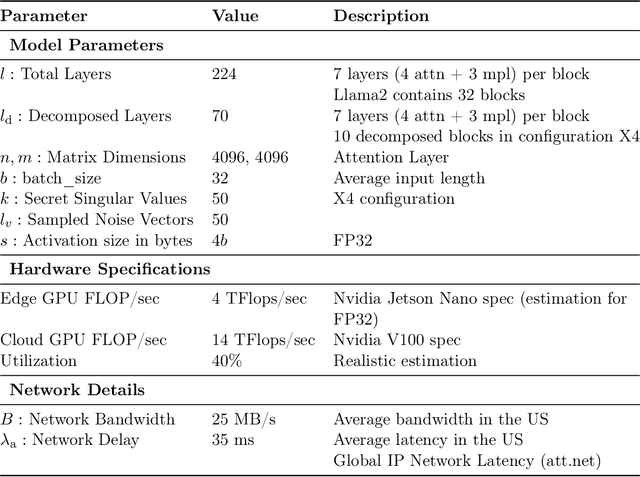
Large language models (LLMs) have recently seen widespread adoption, in both academia and industry. As these models grow, they become valuable intellectual property (IP), reflecting enormous investments by their owners. Moreover, the high cost of cloud-based deployment has driven interest towards deployment to edge devices, yet this risks exposing valuable parameters to theft and unauthorized use. Current methods to protect models' IP on the edge have limitations in terms of practicality, loss in accuracy, or suitability to requirements. In this paper, we introduce a novel hybrid inference algorithm, named SLIP, designed to protect edge-deployed models from theft. SLIP is the first hybrid protocol that is both practical for real-world applications and provably secure, while having zero accuracy degradation and minimal impact on latency. It involves partitioning the model between two computing resources, one secure but expensive, and another cost-effective but vulnerable. This is achieved through matrix decomposition, ensuring that the secure resource retains a maximally sensitive portion of the model's IP while performing a minimal amount of computations, and vice versa for the vulnerable resource. Importantly, the protocol includes security guarantees that prevent attackers from exploiting the partition to infer the secured information. Finally, we present experimental results that show the robustness and effectiveness of our method, positioning it as a compelling solution for protecting LLMs.

Fighting COVID-19 in the Dark: Methodology for Improved Inference Using Homomorphically Encrypted DNN

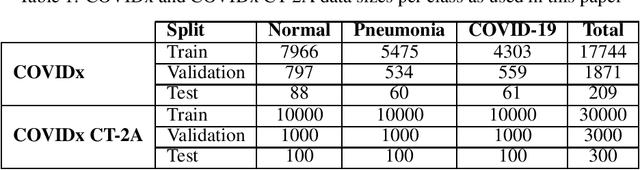
Privacy-preserving deep neural network (DNN) inference is a necessity in different regulated industries such as healthcare, finance, and retail. Recently, homomorphic encryption (HE) has been used as a method to enable analytics while addressing privacy concerns. HE enables secure predictions over encrypted data. However, there are several challenges related to the use of HE, including DNN size limitations and the lack of support for some operation types. Most notably, the commonly used ReLU activation is not supported under some HE schemes. We propose a structured methodology to replace ReLU with a quadratic polynomial activation. To address the accuracy degradation issue, we use a pre-trained model that trains another HE-friendly model, using techniques such as "trainable activation" functions and knowledge distillation. We demonstrate our methodology on the AlexNet architecture, using the chest X-Ray and CT datasets for COVID-19 detection. Our experiments show that by using our approach, the gap between the F1 score and accuracy of the models trained with ReLU and the HE-friendly model is narrowed down to within a mere 1.1 - 5.3 percent degradation.

Tile Tensors: A versatile data structure with descriptive shapes for homomorphic encryption

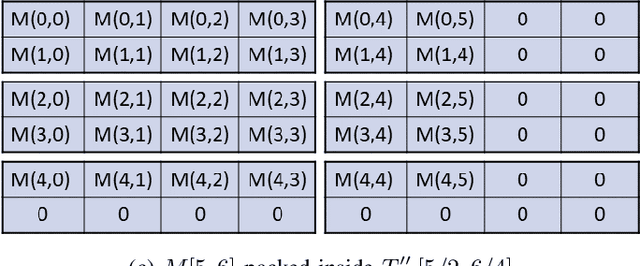
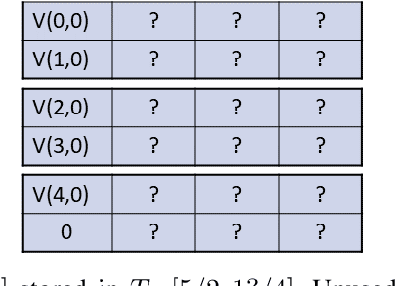
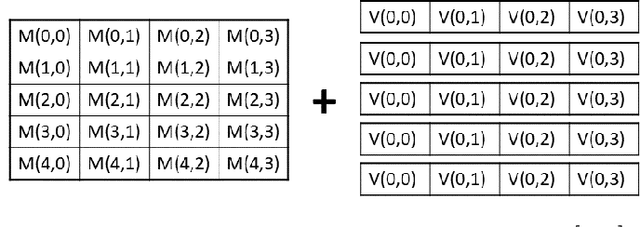
Moving from the theoretical promise of Fully Homomorphic Encryption (FHE) to real-world applications with realistic and acceptable time and memory figures is an on-going challenge. After choosing an appropriate FHE scheme, and before implementing privacy-preserving analytics, one needs an efficient packing method that will optimize use of the ciphertext slots, trading-off size, latency, and throughput. We propose a solution to this challenge. We describe a method for efficiently working with tensors (multi-dimensional arrays) in a system that imposes tiles, i.e., fixed-size vectors. The tensors are packed into tiles and then manipulated via operations on those tiles. We further show a novel and concise notation for describing packing details. Our method reinterprets the tiles as multi-dimensional arrays, and combines them to cover enough space to hold the tensor. An efficient summation algorithm can then sum over any dimension of this construct. We propose a descriptive notation for the shape of this data structure that describes both the original tensor and how it is packed inside the tiles. Our solution can be used to optimize the performance of various algorithms such as consecutive matrix multiplications or neural network inference with varying batch sizes. It can also serve to enhance optimizations done by homomorphic encryption compilers. We describe different applications that take advantage of this data structure through the proposed notation, experiment to evaluate the advantages through different applications, and share our conclusions.