Optimal Transport Tools : A JAX Toolbox for all things Wasserstein

Optimal transport tools (OTT-JAX) is a Python toolbox that can solve optimal transport problems between point clouds and histograms. The toolbox builds on various JAX features, such as automatic and custom reverse mode differentiation, vectorization, just-in-time compilation and accelerators support. The toolbox covers elementary computations, such as the resolution of the regularized OT problem, and more advanced extensions, such as barycenters, Gromov-Wasserstein, low-rank solvers, estimation of convex maps, differentiable generalizations of quantiles and ranks, and approximate OT between Gaussian mixtures. The toolbox code is available at \texttt{https://github.com/ott-jax/ott}

Correcting Nuisance Variation using Wasserstein Distance

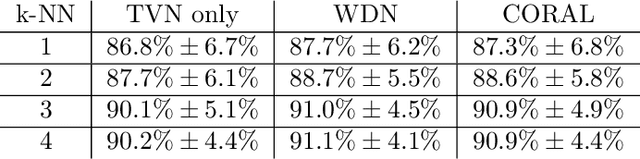
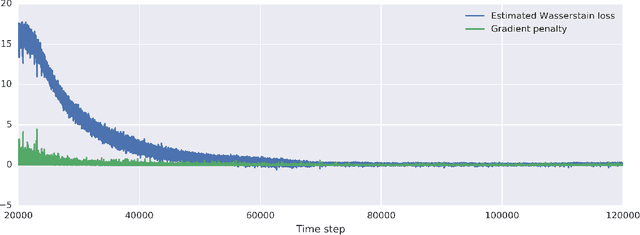
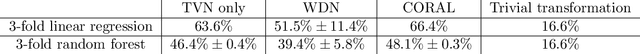
Profiling cellular phenotypes from microscopic imaging can provide meaningful biological information resulting from various factors affecting the cells. One motivating application is drug development: morphological cell features can be captured from images, from which similarities between different drugs applied at different dosages can be quantified. The general approach is to find a function mapping the images to an embedding space of manageable dimensionality whose geometry captures relevant features of the input images. An important known issue for such methods is separating relevant biological signal from nuisance variation. For example, the embedding vectors tend to be more correlated for cells that were cultured and imaged during the same week than for cells from a different week, despite having identical drug compounds applied in both cases. In this case, the particular batch a set of experiments were conducted in constitutes the domain of the data; an ideal set of image embeddings should contain only the relevant biological information (e.g. drug effects). We develop a method for adjusting the image embeddings in order to `forget' domain-specific information while preserving relevant biological information. To do this, we minimize a loss function based on the Wasserstein distance. We find for our transformed embeddings (1) the underlying geometric structure is preserved and (2) less domain-specific information is present.