Optimal Transport Tools : A JAX Toolbox for all things Wasserstein

Optimal transport tools (OTT-JAX) is a Python toolbox that can solve optimal transport problems between point clouds and histograms. The toolbox builds on various JAX features, such as automatic and custom reverse mode differentiation, vectorization, just-in-time compilation and accelerators support. The toolbox covers elementary computations, such as the resolution of the regularized OT problem, and more advanced extensions, such as barycenters, Gromov-Wasserstein, low-rank solvers, estimation of convex maps, differentiable generalizations of quantiles and ranks, and approximate OT between Gaussian mixtures. The toolbox code is available at \texttt{https://github.com/ott-jax/ott}

JKOnet: Proximal Optimal Transport Modeling of Population Dynamics

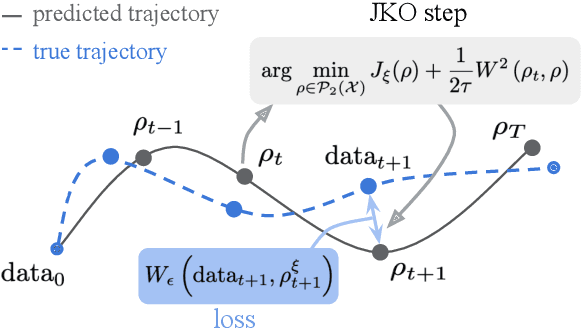
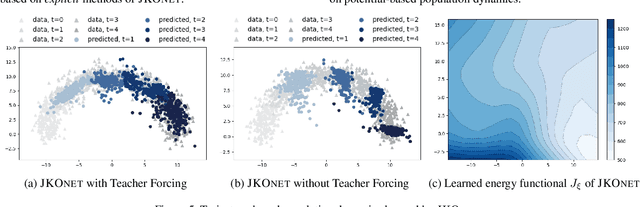
Consider a heterogeneous population of points evolving with time. While the population evolves, both in size and nature, we can observe it periodically, through snapshots taken at different timestamps. Each of these snapshots is formed by sampling points from the population at that time, and then creating features to recover point clouds. While these snapshots describe the population's evolution on aggregate, they do not provide directly insights on individual trajectories. This scenario is encountered in several applications, notably single-cell genomics experiments, tracking of particles, or when studying crowd motion. In this paper, we propose to model that dynamic as resulting from the celebrated Jordan-Kinderlehrer-Otto (JKO) proximal scheme. The JKO scheme posits that the configuration taken by a population at time $t$ is one that trades off a decrease w.r.t. an energy (the model we seek to learn) penalized by an optimal transport distance w.r.t. the previous configuration. To that end, we propose JKOnet, a neural architecture that combines an energy model on measures, with (small) optimal displacements solved with input convex neural networks (ICNN). We demonstrate the applicability of our model to explain and predict population dynamics.