A Metric Driven Approach to Mixed Precision Training

As deep learning methodologies have developed, it has been generally agreed that increasing neural network size improves model quality. However, this is at the expense of memory and compute requirements, which also need to be increased. Various efficiency techniques have been proposed to rein in hardware costs, one being the use of low precision numerics. Recent accelerators have introduced several different 8-bit data types to help accommodate DNNs in terms of numerics. In this paper, we identify a metric driven methodology to aid in the choice of numerics. We demonstrate how such a methodology can help scale training of a language representation model. The technique can be generalized to other model architectures.

Correcting Nuisance Variation using Wasserstein Distance

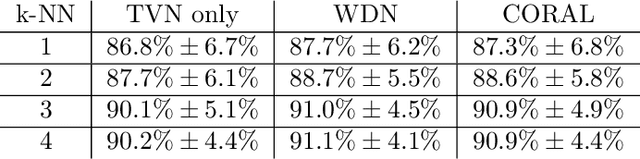
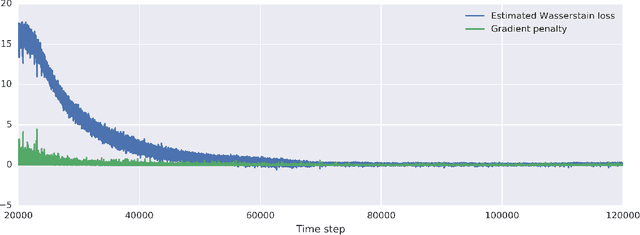
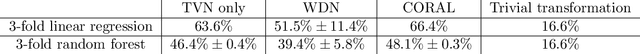
Profiling cellular phenotypes from microscopic imaging can provide meaningful biological information resulting from various factors affecting the cells. One motivating application is drug development: morphological cell features can be captured from images, from which similarities between different drugs applied at different dosages can be quantified. The general approach is to find a function mapping the images to an embedding space of manageable dimensionality whose geometry captures relevant features of the input images. An important known issue for such methods is separating relevant biological signal from nuisance variation. For example, the embedding vectors tend to be more correlated for cells that were cultured and imaged during the same week than for cells from a different week, despite having identical drug compounds applied in both cases. In this case, the particular batch a set of experiments were conducted in constitutes the domain of the data; an ideal set of image embeddings should contain only the relevant biological information (e.g. drug effects). We develop a method for adjusting the image embeddings in order to `forget' domain-specific information while preserving relevant biological information. To do this, we minimize a loss function based on the Wasserstein distance. We find for our transformed embeddings (1) the underlying geometric structure is preserved and (2) less domain-specific information is present.