From Temporal to Contemporaneous Iterative Causal Discovery in the Presence of Latent Confounders

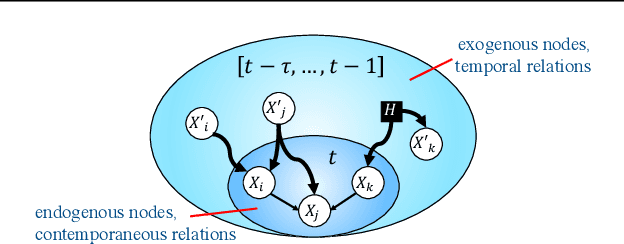
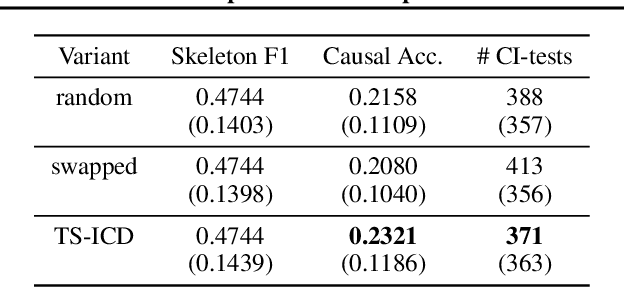
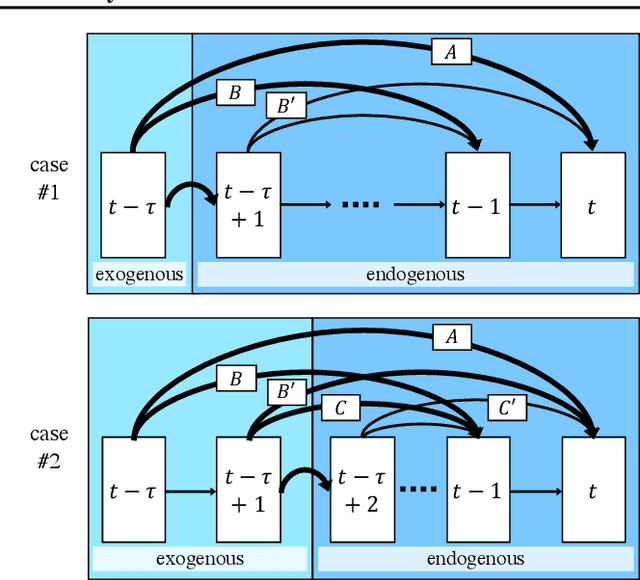
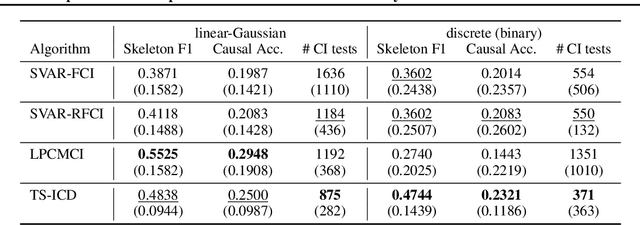
We present a constraint-based algorithm for learning causal structures from observational time-series data, in the presence of latent confounders. We assume a discrete-time, stationary structural vector autoregressive process, with both temporal and contemporaneous causal relations. One may ask if temporal and contemporaneous relations should be treated differently. The presented algorithm gradually refines a causal graph by learning long-term temporal relations before short-term ones, where contemporaneous relations are learned last. This ordering of causal relations to be learnt leads to a reduction in the required number of statistical tests. We validate this reduction empirically and demonstrate that it leads to higher accuracy for synthetic data and more plausible causal graphs for real-world data compared to state-of-the-art algorithms.

Wall Street Tree Search: Risk-Aware Planning for Offline Reinforcement Learning

Offline reinforcement-learning (RL) algorithms learn to make decisions using a given, fixed training dataset without the possibility of additional online data collection. This problem setting is captivating because it holds the promise of utilizing previously collected datasets without any costly or risky interaction with the environment. However, this promise also bears the drawback of this setting. The restricted dataset induces subjective uncertainty because the agent can encounter unfamiliar sequences of states and actions that the training data did not cover. Moreover, inherent system stochasticity further increases uncertainty and aggravates the offline RL problem, preventing the agent from learning an optimal policy. To mitigate the destructive uncertainty effects, we need to balance the aspiration to take reward-maximizing actions with the incurred risk due to incorrect ones. In financial economics, modern portfolio theory (MPT) is a method that risk-averse investors can use to construct diversified portfolios that maximize their returns without unacceptable levels of risk. We integrate MPT into the agent's decision-making process to present a simple-yet-highly-effective risk-aware planning algorithm for offline RL. Our algorithm allows us to systematically account for the \emph{estimated quality} of specific actions and their \emph{estimated risk} due to the uncertainty. We show that our approach can be coupled with the Transformer architecture to yield a state-of-the-art planner for offline RL tasks, maximizing the return while significantly reducing the variance.

Learning Control by Iterative Inversion

We formulate learning for control as an $\textit{inverse problem}$ -- inverting a dynamical system to give the actions which yield desired behavior. The key challenge in this formulation is a $\textit{distribution shift}$ -- the learning agent only observes the forward mapping (its actions' consequences) on trajectories that it can execute, yet must learn the inverse mapping for inputs-outputs that correspond to a different, desired behavior. We propose a general recipe for inverse problems with a distribution shift that we term $\textit{iterative inversion}$ -- learn the inverse mapping under the current input distribution (policy), then use it on the desired output samples to obtain new inputs, and repeat. As we show, iterative inversion can converge to the desired inverse mapping, but under rather strict conditions on the mapping itself. We next apply iterative inversion to learn control. Our input is a set of demonstrations of desired behavior, given as video embeddings of trajectories, and our method iteratively learns to imitate trajectories generated by the current policy, perturbed by random exploration noise. We find that constantly adding the demonstrated trajectory embeddings $\textit{as input}$ to the policy when generating trajectories to imitate, a-la iterative inversion, steers the learning towards the desired trajectory distribution. To the best of our knowledge, this is the first exploration of learning control from the viewpoint of inverse problems, and our main advantage is simplicity -- we do not require rewards, and only employ supervised learning, which easily scales to state-of-the-art trajectory embedding techniques and policy representations. With a VQ-VAE embedding, and a transformer-based policy, we demonstrate non-trivial continuous control on several tasks. We also report improved performance on imitating diverse behaviors compared to reward based methods.

Validate on Sim, Detect on Real -- Model Selection for Domain Randomization

A practical approach to learning robot skills, often termed sim2real, is to train control policies in simulation and then deploy them on a real robot. Popular techniques to improve the sim2real transfer build on domain randomization (DR): Training the policy on a diverse set of randomly generated domains with the hope of better generalization to the real world. Due to the large number of hyper-parameters in both the policy learning and DR algorithms, one often ends up with a large number of trained models, where choosing the best model among them demands costly evaluation on the real robot. In this work we ask: Can we rank the policies without running them in the real world? Our main idea is that a predefined set of real world data can be used to evaluate all policies, using out-of-distribution detection (OOD) techniques. In a sense, this approach can be seen as a "unit test" to evaluate policies before any real world execution. However, we find that by itself, the OOD score can be inaccurate and very sensitive to the particular OOD method. Our main contribution is a simple-yet-effective policy score that combines OOD with an evaluation in simulation. We show that our score - VSDR - can significantly improve the accuracy of policy ranking without requiring additional real world data. We evaluate the effectiveness of VSDR on sim2real transfer in a robotic grasping task with image inputs. We extensively evaluate different DR parameters and OOD methods, and show that VSDR improves policy selection across the board. More importantly, our method achieves significantly better ranking, and uses significantly less data compared to baselines.

Iterative Causal Discovery in the Possible Presence of Latent Confounders and Selection Bias

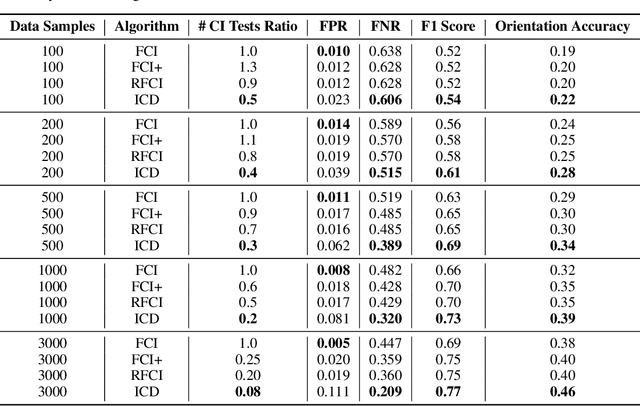
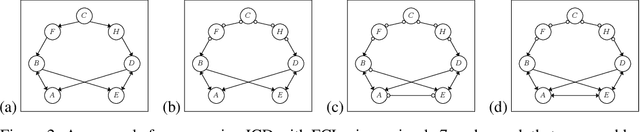
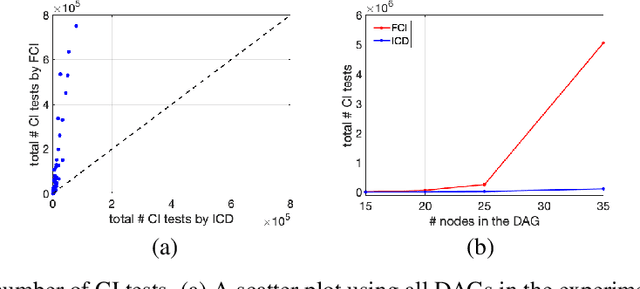
We present a sound and complete algorithm, called iterative causal discovery (ICD), for recovering causal graphs in the presence of latent confounders and selection bias. ICD relies on the causal Markov and faithfulness assumptions and recovers the equivalence class of the underlying causal graph. It starts with a complete graph, and consists of a single iterative stage that gradually refines this graph by identifying conditional independence (CI) between connected nodes. Independence and causal relations entailed after any iteration are correct, rendering ICD anytime. Essentially, we tie the size of the CI conditioning set to its distance on the graph from the tested nodes, and increase this value in the successive iteration. Thus, each iteration refines a graph that was recovered by previous iterations having smaller conditioning sets -- a higher statistical power -- which contributes to stability. We demonstrate empirically that ICD requires significantly fewer CI tests and learns more accurate causal graphs compared to FCI, FCI+, and RFCI algorithms.

Improving Efficiency and Accuracy of Causal Discovery Using a Hierarchical Wrapper

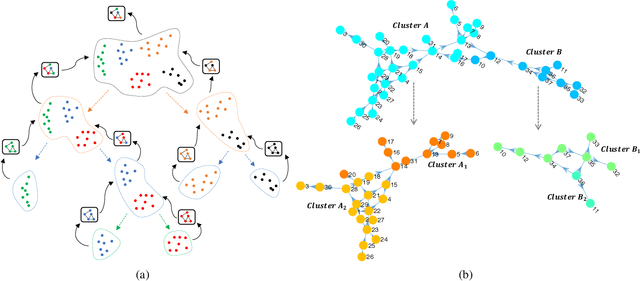
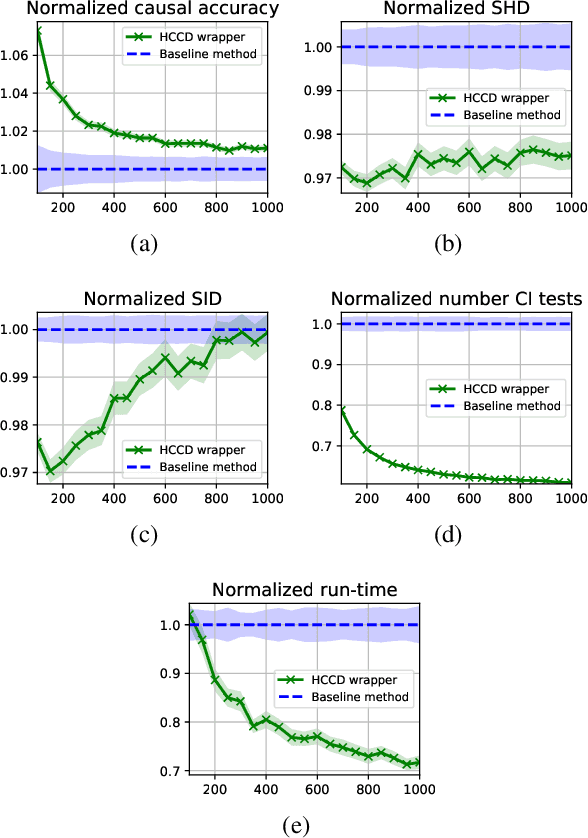
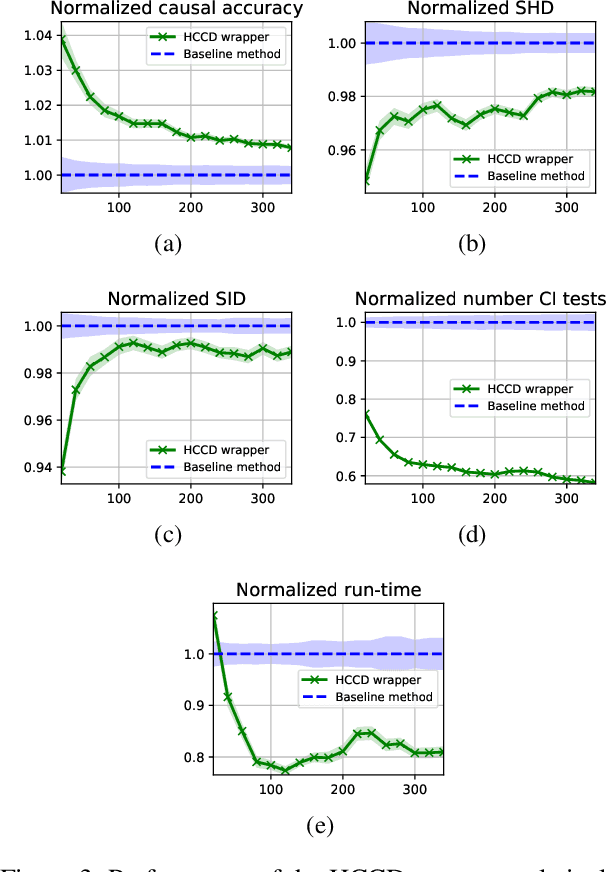
Causal discovery from observational data is an important tool in many branches of science. Under certain assumptions it allows scientists to explain phenomena, predict, and make decisions. In the large sample limit, sound and complete causal discovery algorithms have been previously introduced, where a directed acyclic graph (DAG), or its equivalence class, representing causal relations is searched. However, in real-world cases, only finite training data is available, which limits the power of statistical tests used by these algorithms, leading to errors in the inferred causal model. This is commonly addressed by devising a strategy for using as few as possible statistical tests. In this paper, we introduce such a strategy in the form of a recursive wrapper for existing constraint-based causal discovery algorithms, which preserves soundness and completeness. It recursively clusters the observed variables using the normalized min-cut criterion from the outset, and uses a baseline causal discovery algorithm during backtracking for learning local sub-graphs. It then combines them and ensures completeness. By an ablation study, using synthetic data, and by common real-world benchmarks, we demonstrate that our approach requires significantly fewer statistical tests, learns more accurate graphs, and requires shorter run-times than the baseline algorithm.

Efficient Self-Supervised Data Collection for Offline Robot Learning

A practical approach to robot reinforcement learning is to first collect a large batch of real or simulated robot interaction data, using some data collection policy, and then learn from this data to perform various tasks, using offline learning algorithms. Previous work focused on manually designing the data collection policy, and on tasks where suitable policies can easily be designed, such as random picking policies for collecting data about object grasping. For more complex tasks, however, it may be difficult to find a data collection policy that explores the environment effectively, and produces data that is diverse enough for the downstream task. In this work, we propose that data collection policies should actively explore the environment to collect diverse data. In particular, we develop a simple-yet-effective goal-conditioned reinforcement-learning method that actively focuses data collection on novel observations, thereby collecting a diverse data-set. We evaluate our method on simulated robot manipulation tasks with visual inputs and show that the improved diversity of active data collection leads to significant improvements in the downstream learning tasks.

A Single Iterative Step for Anytime Causal Discovery

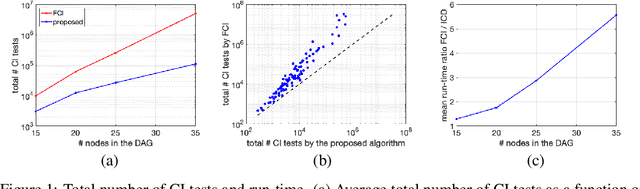
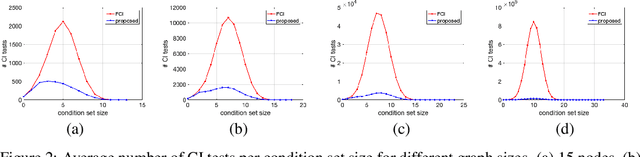
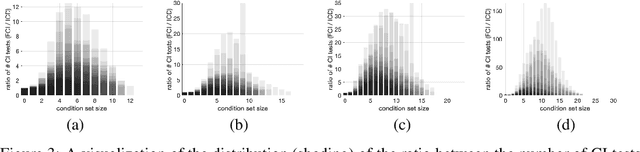
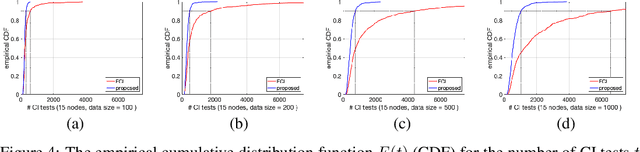
We present a sound and complete algorithm for recovering causal graphs from observed, non-interventional data, in the possible presence of latent confounders and selection bias. We rely on the causal Markov and faithfulness assumptions and recover the equivalence class of the underlying causal graph by performing a series of conditional independence (CI) tests between observed variables. We propose a single step that is applied iteratively, such that the independence and causal relations entailed from the resulting graph, after any iteration, is correct and becomes more informative with successive iteration. Essentially, we tie the size of the CI condition set to its distance from the tested nodes on the resulting graph. Each iteration refines the skeleton and orientation by performing CI tests having condition sets that are larger than in the preceding iteration. In an iteration, condition sets of CI tests are constructed from nodes that are within a specified search distance, and the sizes of these condition sets is equal to this search distance. The algorithm then iteratively increases the search distance along with the condition set sizes. Thus, each iteration refines a graph, that was recovered by previous iterations having smaller condition sets -- having a higher statistical power. We demonstrate that our algorithm requires significantly fewer CI tests and smaller condition sets compared to the FCI algorithm. This is evident for both recovering the true underlying graph using a perfect CI oracle, and accurately estimating the graph using limited observed data.

Neural Network Distiller: A Python Package For DNN Compression Research

This paper presents the philosophy, design and feature-set of Neural Network Distiller, an open-source Python package for DNN compression research. Distiller is a library of DNN compression algorithms implementations, with tools, tutorials and sample applications for various learning tasks. Its target users are both engineers and researchers, and the rich content is complemented by a design-for-extensibility to facilitate new research. Distiller is open-source and is available on Github at https://github.com/NervanaSystems/distiller.

Modeling Uncertainty by Learning a Hierarchy of Deep Neural Connections

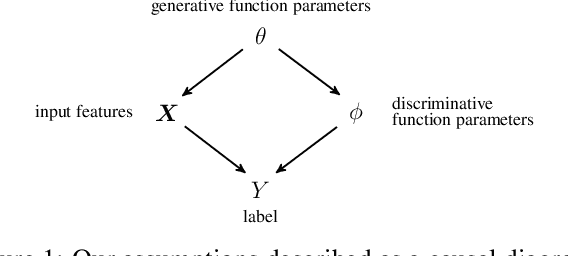
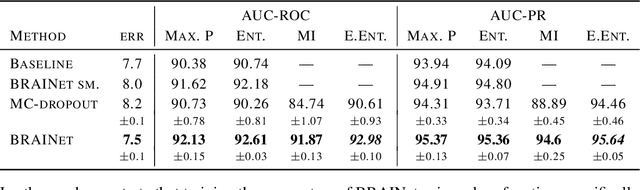
Quantifying and measuring uncertainty in deep neural networks, despite recent important advances, is still an open problem. Bayesian neural networks are a powerful solution, where the prior over network weights is a design choice, often a normal distribution or other distribution encouraging sparsity. However, this prior is agnostic to the generative process of the input data, which might lead to unwarranted generalization for out-of-distribution tested data. We suggest treating the generative process of the input data as a confounder for the relation between the input and the discriminative function, thereby conditioning the prior of the network weights on the distribution of the input. We propose an algorithm for modeling this confounder through neural connectivity patterns. This approach is ultimately translated into a new deep architecture---a compact hierarchy of networks. We demonstrate that sampling networks from this hierarchy, proportionally to their posterior, is efficient and enables estimating various types of uncertainties. Empirical evaluations of our method demonstrate significant improvement compared to state-of-the-art calibration and out-of-distribution detection methods.